1.cho tam giác ABC có góc A=120 độ. Ở phía ngoài tam giác ABC vẽ tam giác đều BCD. chứng minh rằng : AD= AB+AC.
2.cho hình thang vuông ABCD, AD vuông góc với DC, 2 đường chéo vuông góc với nhau. chứng minh: AD^2 = AB x DC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
9 tháng 6 2016
Gọi giao điểm của hai đường chéo là O giao điểm của hai cạnh bên là S,giao điểm của SO với AB,CD lần lượt là X,Y.
Ta có AX//YC nên theo định lý Ta lét ta có:
\(\frac{AX}{YC}\)=\(\frac{AO}{OC}\)=\(\frac{AB}{DC}\)=\(\frac{AX}{DY}\)
=>YC=DY
Vậy Y là trung điểm của DC.
Ta có AB//DC theo định lý Ta-lét ta có:
\(\frac{AX}{DY}\)=\(\frac{SX}{XY}\)=\(\frac{XB}{YC}\)
mà DY=YC(c/m trên)
=>AX=XB=>X là trung điểm của AB
Vậy giao điểm của SO với AB,CD tại trung điểm của các cạnh đó
=>đpcm
Ta cũng dễ dàng chứng mình được đường thẳng chứa 4 điểm đó là trùng trực của hai cạnh đấy sao khi chừng minh chúng thẳng hàng ở trên nhé!
C
27 tháng 12 2017
Gọi giao điểm của hai đường chéo là O giao điểm của hai cạnh bên là S,giao điểm của SO với AB,CD lần lượt là X,Y.
Ta có AX//YC nên theo định lý Ta lét ta có:
AXYCAXYC=AOOCAOOC=ABDCABDC=AXDYAXDY
=>YC=DY
Vậy Y là trung điểm của DC.
Ta có AB//DC theo định lý Ta-lét ta có:
AXDYAXDY=SXXYSXXY=XBYCXBYC
mà DY=YC(c/m trên)
=>AX=XB=>X là trung điểm của AB
Vậy giao điểm của SO với AB,CD tại trung điểm của các cạnh đó
=>đpcm
DD
Đoàn Đức Hà
Giáo viên
20 tháng 7 2021
Câu 3.
Tam giác \(ABC\)vuông cân tại \(A\)nên \(\widehat{ACB}=45^o\).
Tam giác \(BCD\)vuông cân tại \(B\)nên \(\widehat{BCD}=45^o\).
\(\widehat{ACD}=\widehat{ACB}+\widehat{BCD}=45^o+45^o=90^o\)
\(\Rightarrow AC\perp CD\)
mà \(AC\perp AB\)
nên \(AB//CD\)
suy ra \(ABCD\)là hình thang vuông.
DD
Đoàn Đức Hà
Giáo viên
20 tháng 7 2021
Câu 4.
Kẻ \(BE\perp CD\)khi đó \(\widehat{BED}=90^o\).
Tứ giác \(ABED\)có \(4\)góc vuông nên là hình chữ nhật, mà \(AB=AD\)nên \(ABED\)là hình vuông.
\(BE=DE=AB=2\left(cm\right)\)
\(EC=CD-DE=4-2=2\left(cm\right)\)
Suy ra tam giác \(BEC\)vuông cân tại \(E\)
Suy ra \(\widehat{EBC}=\widehat{ECB}=45^o\)
\(\widehat{ABC}=\widehat{ABE}+\widehat{EBC}=90^o+45^o=135^o\)
CM
30 tháng 7 2019
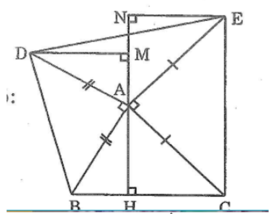
Ta có: ∠(BAH) +∠(BAD) +∠(DAM) =180o(kề bù)
Mà ∠(BAD) =90o⇒∠(BAH) +∠(DAM) =90o(1)
Trong tam giác vuông AMD, ta có:
∠(AMD) =90o⇒∠(DAM) +∠(ADM) =90o(2)
Từ (1) và (2) suy ra: ∠(BAH) =∠(ADM)
Xét hai tam giác vuông AMD và BHA, ta có:
∠(BAH) =∠(ADM)
AB = AD (gt)
Suy ra: ΔAMD= ΔBHA(cạnh huyền, góc nhọn)
Vậy: AH = DM (hai cạnh tương ứng) (3)
16 tháng 11 2017
a) Ta có: góc DAC= góc DAB + góc BAC
góc BAE= góc EAC+ góc CAB
Mà góc DAB= góc EAC=90 độ
=> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE có:
AD=AB
góc DAC= góc BAE
AC=AE
=> tam giác DAC= tam giác BAE ( c.g.c)
=> DC=BE
Gọi I và H lần lượt là giao điểm của DC với AB và BE
Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ
Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)
=> góc DAH= góc BIH
Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE
Các bn xem thử đúng ko nhé , mai mk kiểm tra 45' , cần ý kiến gấp
CM
30 tháng 7 2018
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
