Từ một điểm $A$ nằm ngoài đường tròn tâm $O$ bán kính $R$, kẻ các tiếp tuyến $AB$, $AC$ với đường tròn ($B$, $C$ là tiếp điểm). Trên cung nhỏ $BC$ lấy một điểm $M$ bất kỳ khác $B$ và $C$. Gọi $I$, $K$, $P$ lần lượt là hình chiếu vuông góc của điểm $M$ trên các đường thẳng $AB$, $AC$, $BC$.
1. Chứng minh rằng $AIMK$ là tứ giác nội tiếp.
2. Chứng minh $\widehat{MPK} = \widehat{MBC}$.
3. Xác định vị trí điểm $M$ trên cung nhỏ $BC$ để tích $MI .MK .MP$ đạt giá trị lớn nhất.

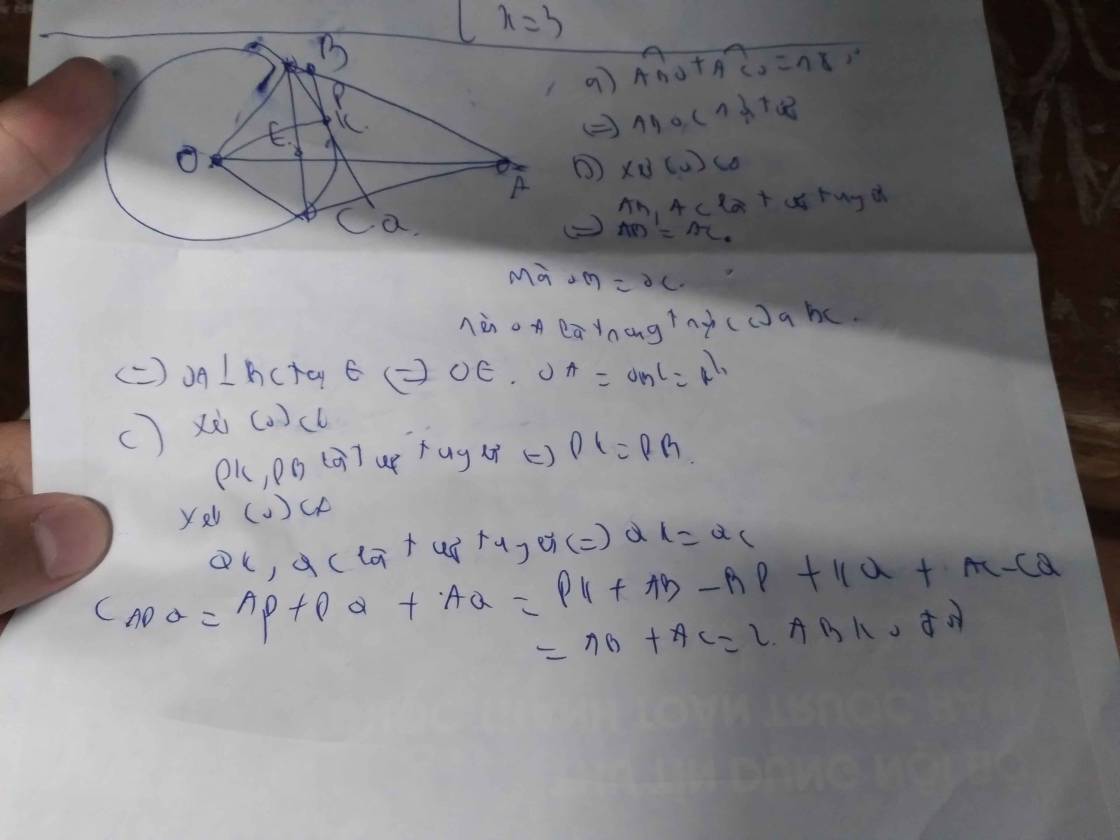
tứ giác AIMK có
góc AIM = góc AKM = 90 độ
suy ra AIMK là tứ giác nội tiếp