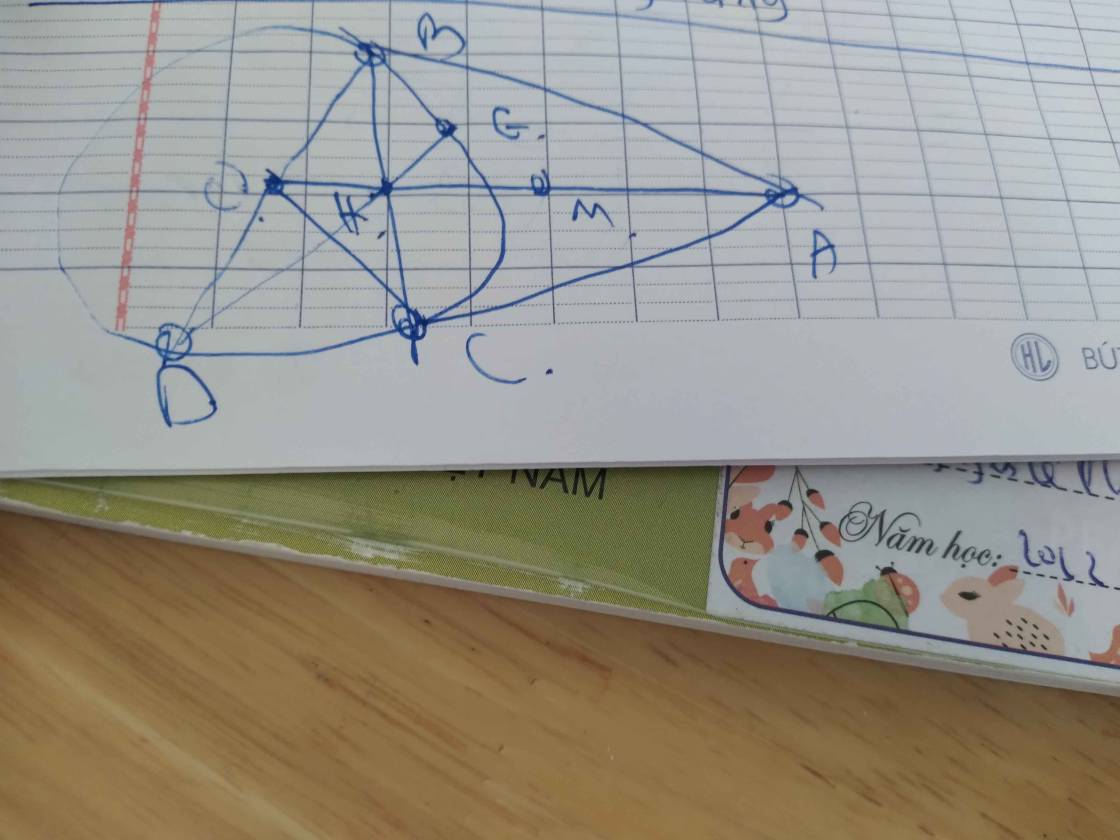
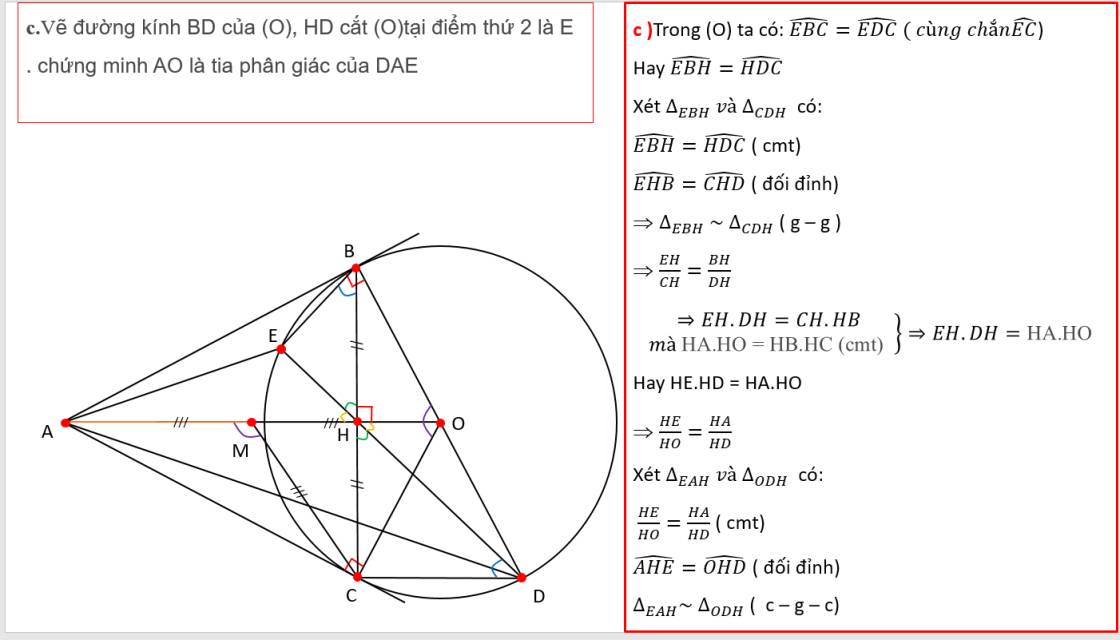
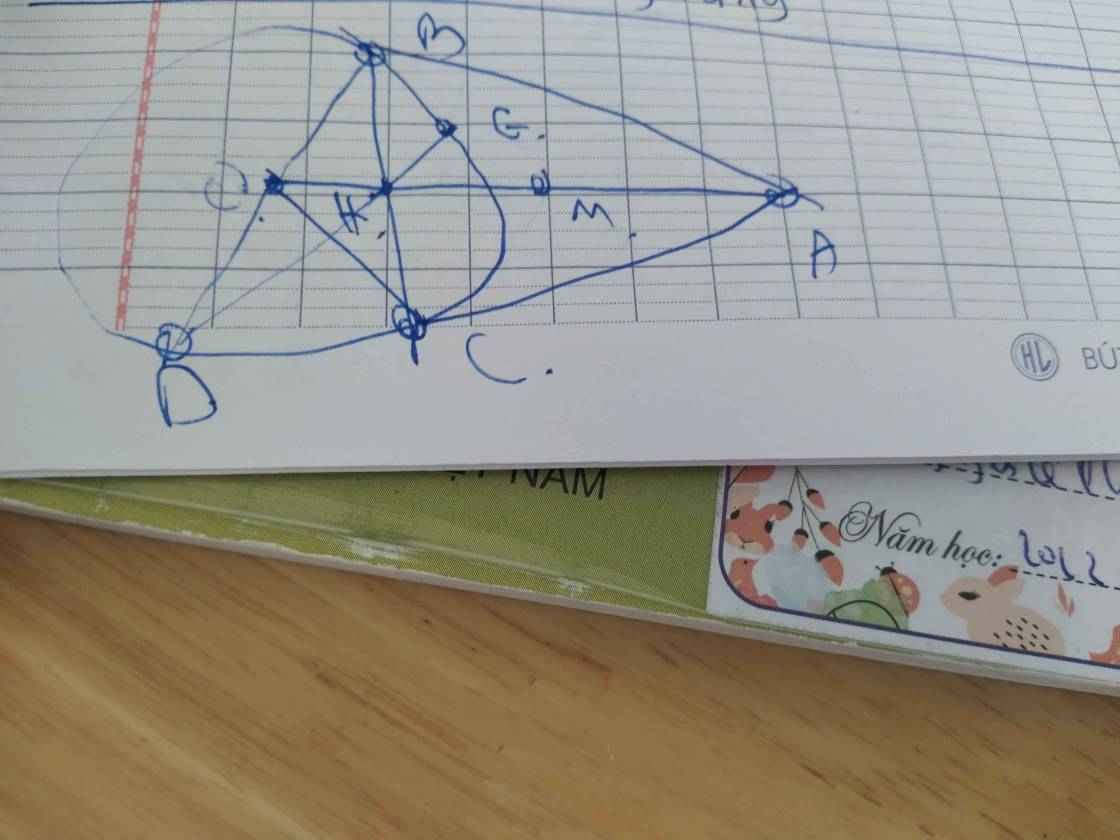
Từ một điểm A ở ngoài đường tròn tâm O kẻ hai tiếp tuyến AB, AC với đường tròn này.
1) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC
2) Gọi điểm D là trung điểm của AC, đoạn thẳng BD cắt đường tròn tâm O tại điểm E, AE cắt đường tròn tâm O tại điểm F Chứng minh AB2 = AE.AF
3) Gọi H là giao điểm của AO và BC. Chứng minh góc DHC = góc DEC



1: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp đường tròn đường kính OA
Tâm là trung điểm của OA
2: Xét ΔABE và ΔAFB có
góc ABE=góc AFB
góc BAE chung
=>ΔABE đồng dạng với ΔAFB
=>AB/AF=AE/AB
=>AB^2=AE*AF