Giúp mình câu 10 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PB
1
20 tháng 12 2022
\(m_{NaCl}=\dfrac{150.10}{100}=15\left(g\right)\\ m_{H_2O}=150-15=135\left(g\right)\)
Đong 15 gam NaCl khan, 135 gam nước cho sẵn vào cốc nước. Sau đó hóa tan 15 gam NaCl vào nước, dùng đũa thủy tinh khuấy đều thu được dd như theo yêu cầu của đề bài
20 tháng 2 2022
Câu 10:
a: \(\Leftrightarrow-x^3+8x^3-12x^2+6x-1+1-3x+3x^2-x^3=0\)
\(\Leftrightarrow6x^3-9x^2+3x=0\)
\(\Leftrightarrow3x\left(2x^2-3x+1\right)=0\)
\(\Leftrightarrow x\left(2x-1\right)\left(x-1\right)=0\)
hay \(x\in\left\{0;\dfrac{1}{2};1\right\}\)
b: Đặt 3x-1=a; x-3=b
Theo đề, ta có: \(a^3+b^3-\left(a+b\right)^3=0\)
\(\Leftrightarrow a^3+b^3-a^3-b^3-3a^2b-3ab^2=0\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x-3=0\\4-4x=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{1}{3};3;1\right\}\)
15 tháng 5 2022
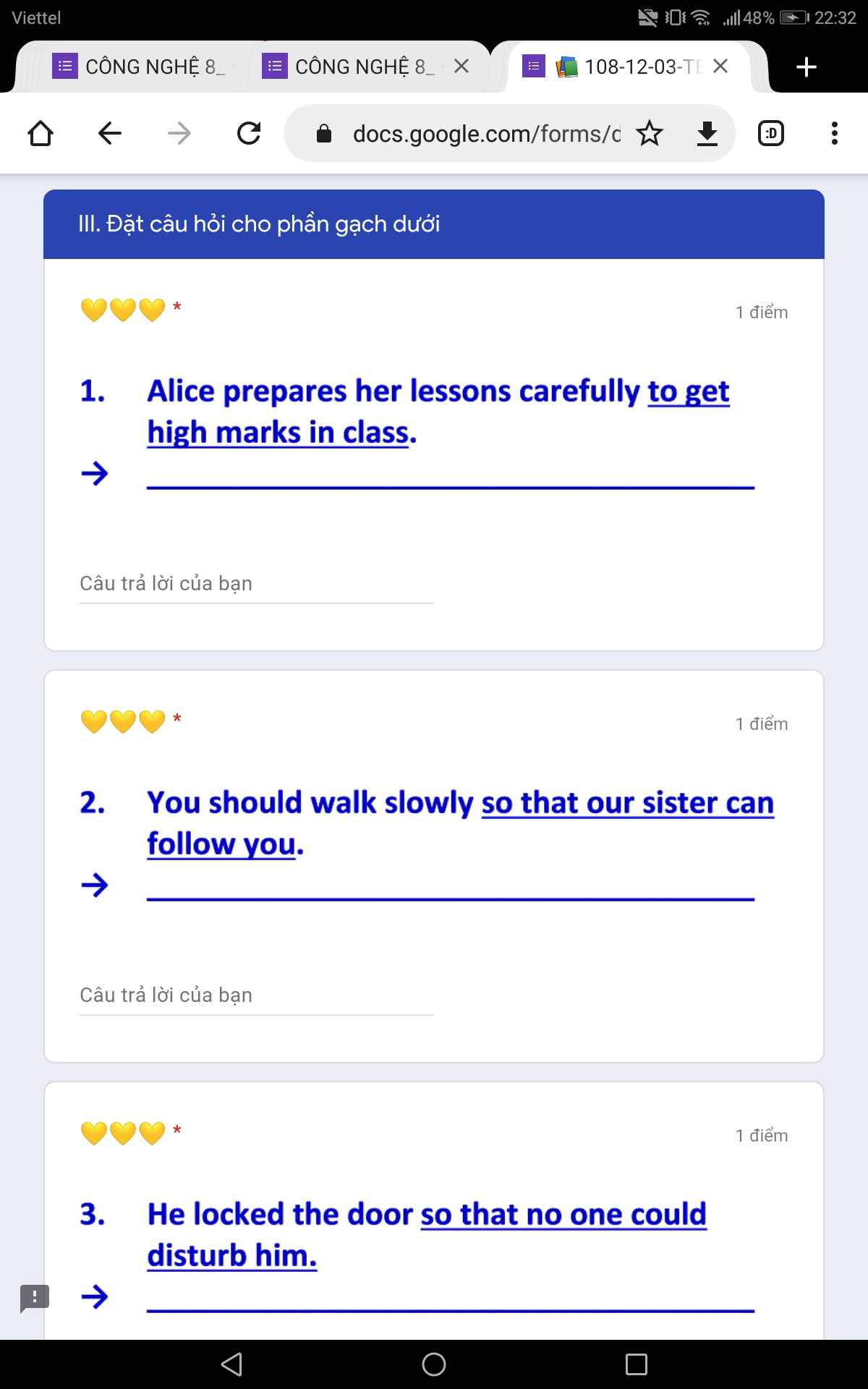
10. A sick child requires more care and attention than a healthy child
chúc e học tốt!
25 tháng 6 2021
7)Đk \(x\le2\)
Pt \(\Leftrightarrow x^2-x+8=4-2x\)
\(\Leftrightarrow x^2+x+4=0\)
\(\Delta=-15< 0\) => vô nghiệm
Vậy pt vô nghiệm
10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)
\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)
\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)
Vậy \(S=\left\{24\right\}\)
20 tháng 5 2021
1D 2B 3C 4A 5A 6C 7A 8A 9B 10A 11C 12D 13D 14D 15A 16D 17A 18C 19C 20D 21D 22C 23C 24A 25B 26C 27D 28B 29C
AH
Akai Haruma
Giáo viên
15 tháng 6 2021
Câu 10:
$\sin ^2x=0\Leftrightarrow \sin x=0$
$\Rightarrow x=k\pi$ với $k$ nguyên.
Trong các khoảng đã cho chỉ có khoảng ở đáp án A chứa $k\pi$ với $k$ nguyên.
AH
Akai Haruma
Giáo viên
15 tháng 6 2021
Câu 11:
PT\(\Leftrightarrow 2\sin x\cos x-\sin x-2+4\cos x=0\)
\(\Leftrightarrow 2\cos x(\sin x+2)-(\sin x+2)=0\)
\(\Leftrightarrow (2\cos x-1)(\sin x+2)=0\)
Vì $\sin x\geq -1$ nên $\sin x+2\geq 1>0$
$\Rightarrow 2\cos x-1=0$
$\Leftrightarrow \cos x=\frac{1}{2}=\cos \frac{\pi}{3}$
$\Rightarrow x=\frac{\pi}{3}+2k\pi$ hoặc $x=-\frac{\pi}{3} +2k\pi$ với $k$ nguyên.
Đáp án B.
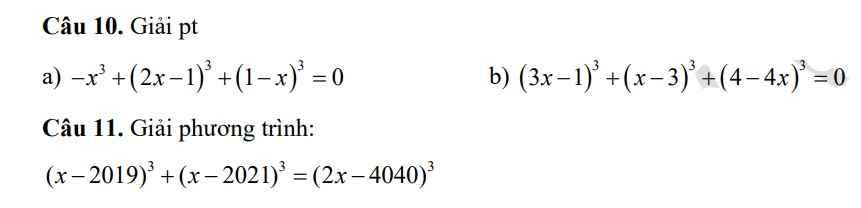
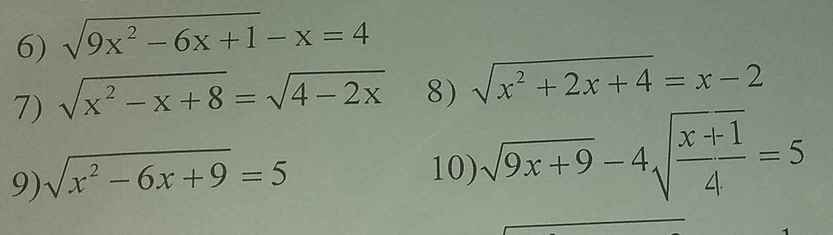
\(S=\int\limits^2_{-3}\left|f\left(x\right)\right|dx=-\int\limits^1_{-3}f\left(x\right)dx+\int\limits^2_1f\left(x\right)dx\)
(Phần nằm dưới trục hoành thêm dấu - đằng trước, phần nằm trên trục hoành giữ nguyên dấu)