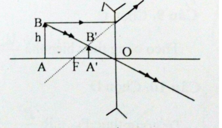
Đặt một vật sáng AB trước một thấu kính phân kỳ thì cho ảnh A'B' (AB vuông góc với trục chính, điểm A nằm trên trục chình)
a) cm AA'=\(\dfrac{OA^2}{AO+OF'}\)
B) CM \(BB'=\dfrac{OA\sqrt{OA^2+AB^2}}{OA+OF'}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
17 tháng 1 2017
Ta có ảnh của một vật qua thấu kính phân kì luôn là ảnh ảo, cùng chiều và nhỏ hơn vật.
Đáp án: B
11 tháng 3 2022
Bài 2.
Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\)
\(\Rightarrow d'=60cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{1,5}{h'}=\dfrac{30}{60}\Rightarrow h'=3cm\)
VT
19 tháng 10 2019
Đáp án D
Dựa vào hình vẽ, Xét các tam giác đồng dạng OAB và OA’B’ ta có:
A'B'/AB = OA'/OA = d'/d = 1/3
OA = d = 3d’ = 3.12 = 36 (cm)
HT
9 tháng 5 2021
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow-\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(d-\left|d'\right|=10\Leftrightarrow d+d'=10\left(d'< 0\right)\)
\(\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{-20.\left(10-d\right)}{10-d+20}=\dfrac{20d-200}{30-d}\Leftrightarrow30d-d^2=20d-200\Leftrightarrow d=...\left(cm\right)\)
VT
27 tháng 6 2018
Đáp án: B
Vì vật sáng đặt ở mọi vị trí trước thấu kính phân kì luôn cho ảnh ảo, cùng chiều, nhỏ hơn vật và luôn nằm trong khoảng tiêu cự của thấu kính. Nên ảnh A ' B ' là ảnh ảo, cùng chiều với vật và nhỏ hơn vật.
