Chứng minh rằng kết quả của phép tính 0.3(19831983+19171917) là 1 số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
PN
0


CM
30 tháng 11 2017
Theo đề bài ta có:
x . − 6 − 23 = 12 + x − 6 x − x = 12 + 23 − 7 x = 35 ⇒ x = − 5

CM
25 tháng 9 2019
a) Ta có 5 = 1.5 = 5.1 = (-1).(-5) = (-5).(-1).
Suy ra các cặp số (x ; y) thỏa mãn là:
(1; 5),(5; 1), (-1; -5), (-5; -1).
b) (l;8),(8;l), (-l; -8)/(-8;- l);(2;4), (4;2), (-2;-4);(-4;-2).
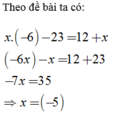
\(0.3\left(1983^{1983}+1917^{1917}\right)\)
\(=0\)
Vậy kết quả của phép tính trên là 1 số nguyên
Muốn chứng tỏ 0,3 * (1983^1983 – 19171917) là số nguyên ta hãy chứng tỏ biểu thức 1983^1983 – 1917^1917 chia hết cho 10, hay nói cách khác biểu thức đó có kết quả là một số có chữ số tận cùng là 0.
Nhận thấy: 19834 có chữ số tận cùng bằng 1
19833 có chữ số tận cùng bằng 7
Nên 19831983 = (19834)495 * 19833 = 1983(4 * 495) + 3 có chữ số tận cùng là 7.
Nhận thấy 19174 có chữ số tận cùng bằng 1
Nên 19171917 = (19174)479 * 1917 có chữ số tận cùng là 7.
Do đó, hiệu số của biểu thức (19831983 – 19171917) sẽ có chữ số tận cùng là 0.
Vậy đáp số của phép tính 0,3 * (19831983 – 19171917) là số nguyên.
Lưu ý: Bài toán này có thể dùng nhị thức Newton để chứng minh đáp số của biểu thức