1. cho x,y > 0 thỏa mãn 2x2 + 2y2 = 5xy. tính giá trị biểu thức M = \(\frac{x+y}{x-y}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2x2 + 2y2 = 5xy
=> 2x2 + 2y2 - 5xy = 0
=> (x - 2y)(2x - y) = 0
x = 2y (loại)
y = 2x
E = \(\dfrac{x+2x}{x-2x}\)=-3

Đáp án B.
Ta có 4 = 2 x + 2 y ≥ 2 2 x . 2 y = 2 2 x + y
⇔ 4 ≥ 2 x + y ⇔ x + y ≤ 2 .
Suy ra x y ≤ x + y 2 2 = 1
Khi đó
P = 2 x 3 + y 3 + 4 x 2 y 2 + 10 x y 2 x + y x + y 2 - 3 x y + 2 x y 2 + 10 x y
≤ 4 4 - 3 x y + 4 x 2 y 2 + 10 x y
= 16 + 2 x 2 y 2 + 2 x y x y - 1 ≤ 18
Vậy Pmax = 18 khi x = y = 1.

Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737

Ta có y= 3-x≥ 1 nên x≤ 2 do đó : x
Khi đó P= x3+ 2( 3-x) 2+ 3x2+4x( 3-x) -5x= x3+x2-5x+18
Xét hàm số f(x) = x3+x2-5x+18 trên đoạn [0 ; 2] ta có:
f ' ( x ) = 3 x 2 + 2 x - 5 ⇒ f ' ( x ) = 0 x ∈ ( 0 ; 2 ) ⇔
F(0) =18; f(1) = 15; f(2) =20
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P lần lượt bằng 20 và 15.
Chọn B.
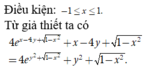
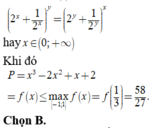
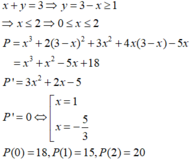

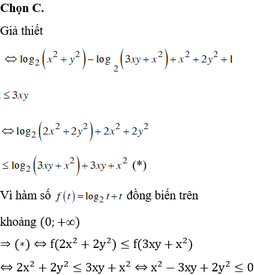
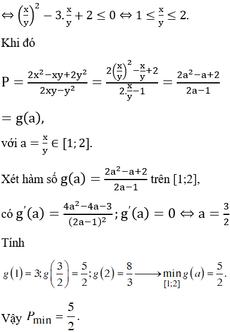
ta có 2x2+2y2=5xy
=>2(x+y)2=9xy và 2(x-y)2=xy
M2=\(\frac{\left(x+y\right)^2}{\left(x-y\right)^2}=\frac{9xy}{xy}=9\)
vậy M=3 hoặc M=-3
Ta dùng phương pháp tách đa thức thành nhân tử ta được
=> x+y=2x2+2y2=2(x2+y2)=9xy
=> x-y=2x2-2y2=2(x2-y2)=xy=1xy=xy
=>M=(x+y)2/(x-y)2=9xy:xy=9
Nên M= cộng trừ căn bậc 2 của 9