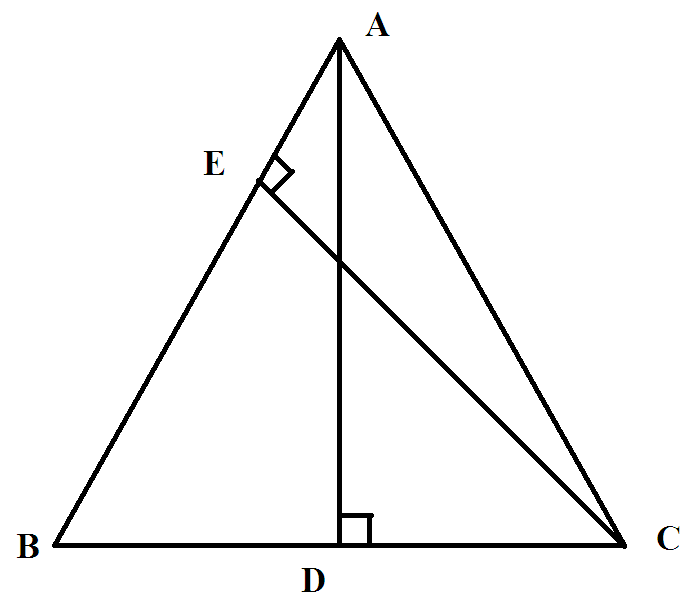
Cho tam giác ABC có AB bằng 9cm, AC bằng 12 cm, BC bằng 15 cm Khẻ đường cao AD
a/ chứng minh: tam giác ADB đồng dạng với tam giác CAB
b/ Vẽ đường phân giác BE \((\)E thuộc AC\()\)
Tính EA,EC
c/ Chứng minh AD\(^2\) \(=\) BD. DC
d/ BE cắt AD tại I tính ID
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
c: BA/BH=BC/BA
=>BA^2=BH*BC

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Ta có: ΔAHB\(\sim\)ΔCAB(cmt)
nên \(\dfrac{AH}{CA}=\dfrac{HB}{AB}=\dfrac{AB}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{AH}{8}=\dfrac{HB}{6}=\dfrac{6}{10}=\dfrac{3}{5}\)
Suy ra: \(\left\{{}\begin{matrix}\dfrac{AH}{8}=\dfrac{3}{5}\\\dfrac{HB}{6}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4.8\left(cm\right)\\HB=3.6\left(cm\right)\end{matrix}\right.\)
Vậy: AH=4,8cm; HB=3,6cm
a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)

a) Xét △ABD và △CBE có:
\(\widehat{ADB}=\widehat{BEC}=90^o\)
\(\widehat{B}chung\)
Nên △ABD ∼ △CBE(g.g)
b)Theo câu a, ta có: △ABD ∼ △CB E
<=>\(\dfrac{AB}{BC}=\dfrac{BD}{BE}\Leftrightarrow AB.BE=BD.BC\)
c)Ta có:
\(BE=\dfrac{BD.BC}{AB}=\dfrac{3.12}{9}=4\left(cm\right)\)

a: Xét ΔADB vuông tại D và ΔCAB vuông tại A có
góc B chung
=>ΔADB đồng dạng với ΔCAB
b: BC=căn 12^2+9^2=15cm
AD=12*9/15=7,2cm

a) Xét ΔCHA và ΔCAB ta có:
\(\widehat{C}\) chung
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\Rightarrow\Delta CHA\)∼\(\Delta CAB\left(g.g\right)\)
b)Xét ΔABC vuông tại A, áp dụng địn lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\\ \Rightarrow AB^2=BC^2-AC^2\)
\(=20^2-16^2\)
\(=144\)
\(\Rightarrow AB=\sqrt{144}=12cm\)
vì ΔCHA∼ΔCAB(cmt)
\(\Rightarrow\dfrac{AB}{AH}=\dfrac{AC}{CH}=\dfrac{BC}{AC}hay\dfrac{12}{AH}=\dfrac{16}{CH}=\dfrac{20}{16}=\dfrac{5}{4}\)
Suy ra:
\(AH=\dfrac{12.4}{5}=9,6cm\)
\(CH=\dfrac{16.4}{5}=12,8cm\)
Xét ΔAHC có AD là phân giác ta có:
\(\dfrac{AH}{HD}=\dfrac{AC}{DC}=\dfrac{AH+AC}{CH}hay\dfrac{9,6}{HD}=\dfrac{16}{DC}=\dfrac{16+9,6}{12,8}=2\)
\(\Rightarrow DC=\dfrac{16}{2}=8cm\)


a, ta có √(92+122)=15 nên theo định lý đảo của định lý pitago => ∠BAC=90 độ
Xét △ADB và △CAB có:
∠BAC=∠BDA(=90 độ), ∠ACB chung => △ADB ∼ △CAB (g.g) (1)
b, BE là đường phân giác của △ABC => \(\dfrac{AB}{AE}=\dfrac{BC}{EC}\)
Gọi AE= x (cm) => EC=12-x (cm)
Ta có: \(\dfrac{9}{x}=\dfrac{15}{12-x}\)=> 108-9x=15x =>108=24x => x=4,5
Vậy EA=4,5 cm, EC=12-4,5=7,5 cm
c, Xét △CAB và △CDA có:
∠BCD chung, ∠ADC=∠BAC(=90 độ) => △CAB ∼ △CDA (g.g) (2)
Từ (1),(2) => △ADB ∼ △CDA (T/c bắc cầu)
=> \(\dfrac{AD}{CD}=\dfrac{DB}{AD}\) => AD2=BD.DC
d, SABC=\(\dfrac{1}{2}.AB.AC\)=\(\dfrac{1}{2}AD.BC\)
=> AB.AC=AD.BC => AD = \(\dfrac{9.12}{15}\)=7,2 cm
Áp dụng định lí Pitago vào △ADC vuông tại D:
AC2=AD2+DC2 => DC=√[122-(7,2)2]=9,6 cm
=> BD=BC-DC=15-9,6=5,4 cm
BI là đường phân giác của △ABD => \(\dfrac{AB}{AI}=\dfrac{BD}{DI}\)
Gọi ID=y (cm) => AI=7,2-y (cm)
Ta có: \(\dfrac{9}{7,2-y}=\dfrac{5,4}{y}\)=> 9y=38,88-5,4y => 14,4y=38,88 => y = 2,7
Nên ID=2,7 cm