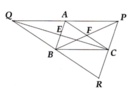
Cho tam giác ABC. Gọi E, F lần lượt là trung điểm của các cạnh AB, AC. Trên tia đối của tia FB lấy điểm P sao cho PF=BF. Trên tia đối của tia EC lấy điểm Q sao cho QE=QC.
a) C/m: AP=AQ
c )C/m BQ//AC và CP//AB
d)Gọi R là giao điểm của 2 đường thẳng PC và QB. C/m rằng chu vi tam giác PQR bằng 2 lần chu vi tam giác ABC
e)Ba đường AR, BP, CQ đồng quy



a) xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=>. tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.
b) xét tam giác BEQ và tam giác AEC có
EQ=EC
BEQ=AEC đối đỉnh
EB=EA
=> tam giác BEQ = tam giác AEC(c.g.c)
=> BQE=AEC(góc tương ứng) mà chúng ở vị trí so le trong nên BQ//AC.
xét tam giác PFC và BFA có:
FA=FC
AFB=CFP
BF=PF
=. tam giác PFC = BFA (c.g.c)
=> FAB = FCB(góc tương ứng)
mà chúng ở vị trí so le trong nên
CP//AB
Có thể loại đường trung bình nữa à Tuân Huỳnh Ngọc Minh???!!!