1806 x 23 ,326 x 142,13840:24 , 28832:272 chi tiết với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
24 tháng 6 2021
1806 28832 : 272
x 24 1632 106
43344 0
Chúc bạn học tốt, k cho mk nhé
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
ST
6
6 tháng 12 2016
4x + 4x+2 = 272
<=> 4x + 4x.42 = 272
<=> 4x ( 1 + 42 ) = 272
<=> 4x = 16
<=> x = 2
VP
1
SS
17 tháng 12 2021
a)305-x-14=48+(-23)
<=>291-x=25
<=>x=291-25
<=>x=266
Vậy x= 266
b)(-14)+x-7=-10
<=>(-21)+x=-10
<=>x=(-10)-(-21)
<=>x=(-10)+21
<=>x=11
Vậy x= 11
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
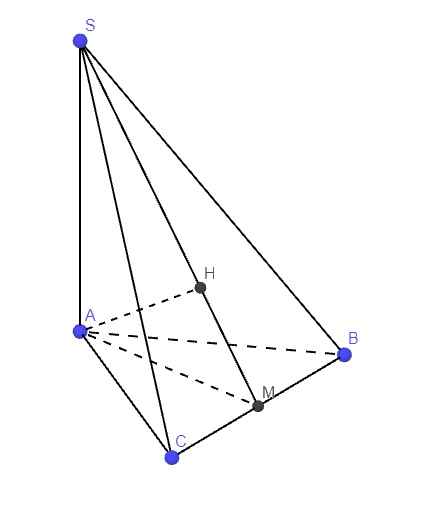
23.
Gọi M là trung điểm BC
Trong mp (SAM), từ A kẻ \(AH\perp SM\) (1)
Ta có: \(AM\perp BC\) (trung tuyến đồng thời là đường cao trong tam giác đều)
Lại có \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAM\right)\Rightarrow BC\perp SH\)
(1);(2) \(\Rightarrow SH\perp\left(SBC\right)\)
\(\Rightarrow SH=d\left(A;\left(SBC\right)\right)\)
\(AM=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Hệ thức lượng trong tam giác vuông SAM:
\(AH=\dfrac{AM.SA}{\sqrt{AM^2+SA^2}}=\dfrac{a\sqrt{66}}{11}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
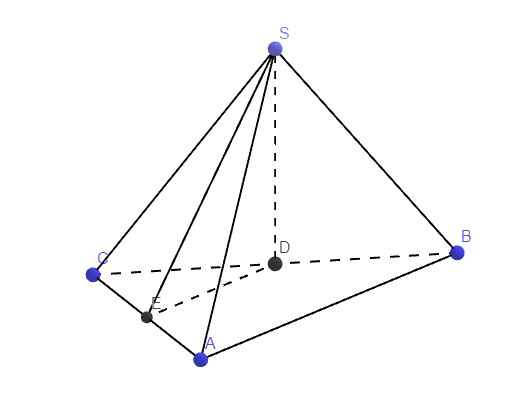
24.
Gọi D, E lần lượt là trung điểm BC, AC
\(\Rightarrow\) DE là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}DE\perp AC\\DE=\dfrac{1}{2}AB\end{matrix}\right.\)
SBC đều \(\Rightarrow SD\perp BC\Rightarrow SD\perp\left(ABC\right)\)
\(\Rightarrow SD\perp AC\)
\(\Rightarrow AC\perp\left(SDE\right)\Rightarrow\widehat{SED}\) là góc giữa (SAC) và (ABC)
\(AB=BC.cos\widehat{ABC}=a.cos30^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow DE=\dfrac{1}{2}AB=\dfrac{a\sqrt{3}}{4}\)
\(SD=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(tan\varphi=tan\widehat{SED}=\dfrac{SD}{DE}=2\)
7 tháng 7 2016
326 x 728 + 327 x 272
= 326 x 728 + 326 x 272 + 272
= 326 x ( 728 +272 ) + 272
= 326 x 1000 + 272
= 326000 + 272
= 326272
6 tháng 7 2016
326 x 728 + 327 x 272
= 326 x 728 + 326 x 272 + 272
= 326 x (728 + 272) + 272
= 326 x 1000 + 272
= 326000 + 272
= 326272
Tham khảo .-.
vô tcn nhìn rõ hơn nhé bạn .-.