Xin giải nhanh giúp em ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



cách 1: x2 + 5x + 4
= x2 + x + 4x + 4
= (x2 + x) (4x + 4)
= x(x + 1) + 4(x + 1)
= (x + 1) (x + 4)
cách 2: x2 + 5x + 4
= x2 + 5x + 5 - 1
= (x2 - 1) (5x + 5)
= (x + 1) (x - 1) + 5(x + 1)
= (x + 1) (x - 1 + 5)
= (x + 1) (x + 4)
cách 3: x2 + 5x + 4
= x2 + 2x + 3x + 1 + 3
= (x2 + 2x + 1) (3x + 3)
= (x + 1)2 + 3(x + 1)
= (x + 1) (x + 1 + 3)
= (x + 1) (x + 4)
cách 4: x2 + 5x + 4
= x2 + \(2\frac{5}{2}x+\frac{25}{4}-\frac{9}{4}\)
= \(\left(x+\frac{5}{2}\right)^2-\left(\frac{3}{2}\right)^2\)
= \(\left(x+\frac{5}{2}-\frac{3}{2}\right)\left(x+\frac{5}{2}+\frac{3}{2}\right)\)
= (x + 1) (x + 4)
t i c k nhé!!! 4656576765876898745724724724745756765786876876876876

Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A



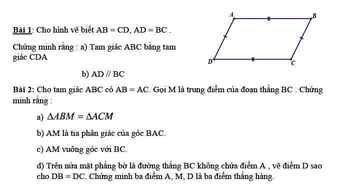
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

a: góc AQE=góc AKE=90 độ
=>AQKE nội tiếp
=>góc KQE=góc KAE=góc BCE
b: góc EAC=góc EBC
góc EBC=góc DKE
=>góc EBC=góc DKE
=>góc EAN=góc EKN
=>AKEN nội tiếp
=>góc ANE+góc AKE=180 độ
=>góc ANE=90 độ
DNCE có góc ENC=góc EDC=90 độ
nên DNEC nội tiếp
+>góc E1=góc C1
mà góc C1=góc A1=góc E2
nên góc E1=góc E2
=>ΔQKE đồng dạng với ΔDNE
=>EN*QK=ND*EQ









c: |3x|=2-x
\(\Leftrightarrow\left\{{}\begin{matrix}x< =2\\\left(3x\right)^2-\left(x-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =2\\\left(3x-x+2\right)\left(3x+x-2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =2\\\left(2x+2\right)\left(4x-2\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{-1;\dfrac{1}{2}\right\}\)
d: |x|=2x+2
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-1\\\left(2x+2\right)^2-x^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-1\\\left(x+2\right)\left(3x+2\right)=0\end{matrix}\right.\Leftrightarrow x=-\dfrac{2}{3}\)