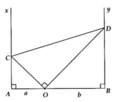
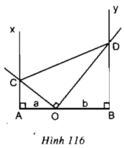
Cho tam giác ABC đều O là trung điểm BC 1 góc XOY = 60 độ quay quanh O, cắt AB ở D, AC ở E.
a) chứng minh tam giác BDO đồng dạng COE.
b) chứng minh tam giác BDO đồng dạng ODE. từ đó suy ra DO là phân giác góc BDE.
c) chứng minh EO là phân giác góc CED
d) kẻ EB vuông góc OD, DQ vuông góc OE. chứng minh rằng DQ=`1/2 DE




-Bài này làm tỷ lần rồi .-.
a) \(\widehat{BDO}=180^0-\widehat{BDO}-\widehat{DOB}=180^0-\widehat{DOE}-\widehat{DOB}=\widehat{COE}\).
\(\Rightarrow\)△BDO∼△COE (g-g).
b) \(\Rightarrow\dfrac{BD}{CO}=\dfrac{DO}{OE}\Rightarrow\dfrac{BD}{BO}=\dfrac{DO}{OE}\)
\(\Rightarrow\)△BDO∼△ODE (c-g-c) \(\Rightarrow\widehat{BDO}=\widehat{ODE}\Rightarrow\)DO là tia p/g góc BDE.
c) △BDO∼△COE \(\Rightarrow\dfrac{BO}{CE}=\dfrac{DO}{OE}\Rightarrow\dfrac{CO}{CE}=\dfrac{DO}{OE}\)
\(\Rightarrow\)△COE∼△ODE (c-g-c) \(\Rightarrow\widehat{CEO}=\widehat{OED}\Rightarrow\)EO là phân giác góc CED.