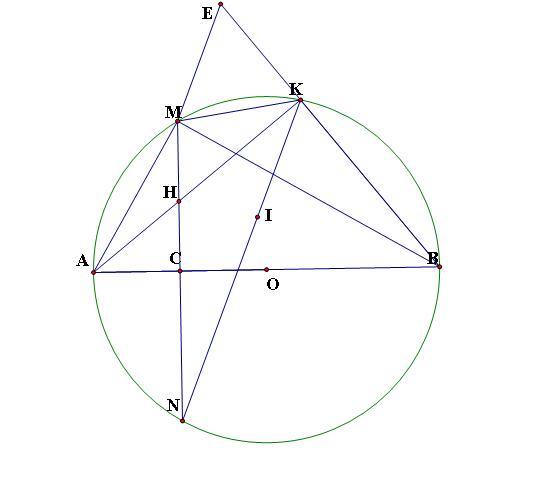
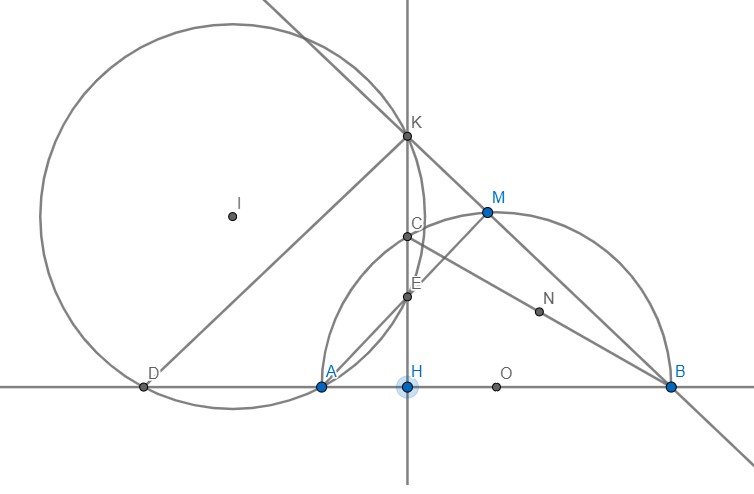
Cho đường tròn tâm (O) đường kính 2R. Gọi C là trung điểm của OA, qua C kẻ đường thẳng vuông góc với OA cắt đường tròn (O) tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K (K khác B và M). Gọi H là giao điểm của AK và MN.
a) Chứng minh tứ giác BCHK nội tiếp đường tròn.
b) Chứng minh AK.AH=R^2.


a: góc AKB=1/2*sđ cung AB=90 độ
góc HCB+góc HKB=180 độ
=>HCBK nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chung
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AB*AC=2R*1/2R=R^2