Cho góc α thoả mãn 0<α<\(\dfrac{\pi}{2}\) và sin α= \(\dfrac{4}{5}\). tính P=cos2α
A. \(P=\dfrac{7}{25}\)
B. \(P=-\dfrac{7}{25}\)
C. \(P=-\dfrac{12}{25}\)
D. \(P=\dfrac{12}{25}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2017
Chọn A.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay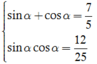 
vào P ta được 
CM
22 tháng 4 2018
Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do 
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy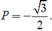 
CM
7 tháng 9 2018
Chọn D.
Xét biểu thức (sin α - cosα ) 2 + (sin α + cosα ) 2 ta có:
(sin α - cosα ) 2 + (sin α + cosα ) 2
= sin 2 α - 2sin α.cosα + cos 2 α + sin 2 α + 2 sin α.cosα + cos 2 α
= 2( sin 2 α + cos 2 α ) =2
⇒ (sin α - cosα ) 2 = 2 - (sin α + cosα ) 2
CM
5 tháng 3 2019
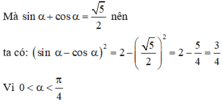
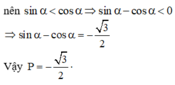
Chọn đáp án C
Với đoạn thẳng AB và góc α ( 0 ° < α < 180 ° ) cho trước thì quỹ tích các điểm M thỏa mãn A M B ^ = α là hai cung chứa góc α dựng trên đoạn AB
Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB . Hai điểm A, B được coi là thuộc quỹ tích
\(P=cos2a=1-2sin^2a=1-2.\left(\dfrac{4}{5}\right)^2=-\dfrac{7}{25}\)