Bổ Toán Bổ Đề Về Tính Chất Đường Phân Giác Trong Tam Giác
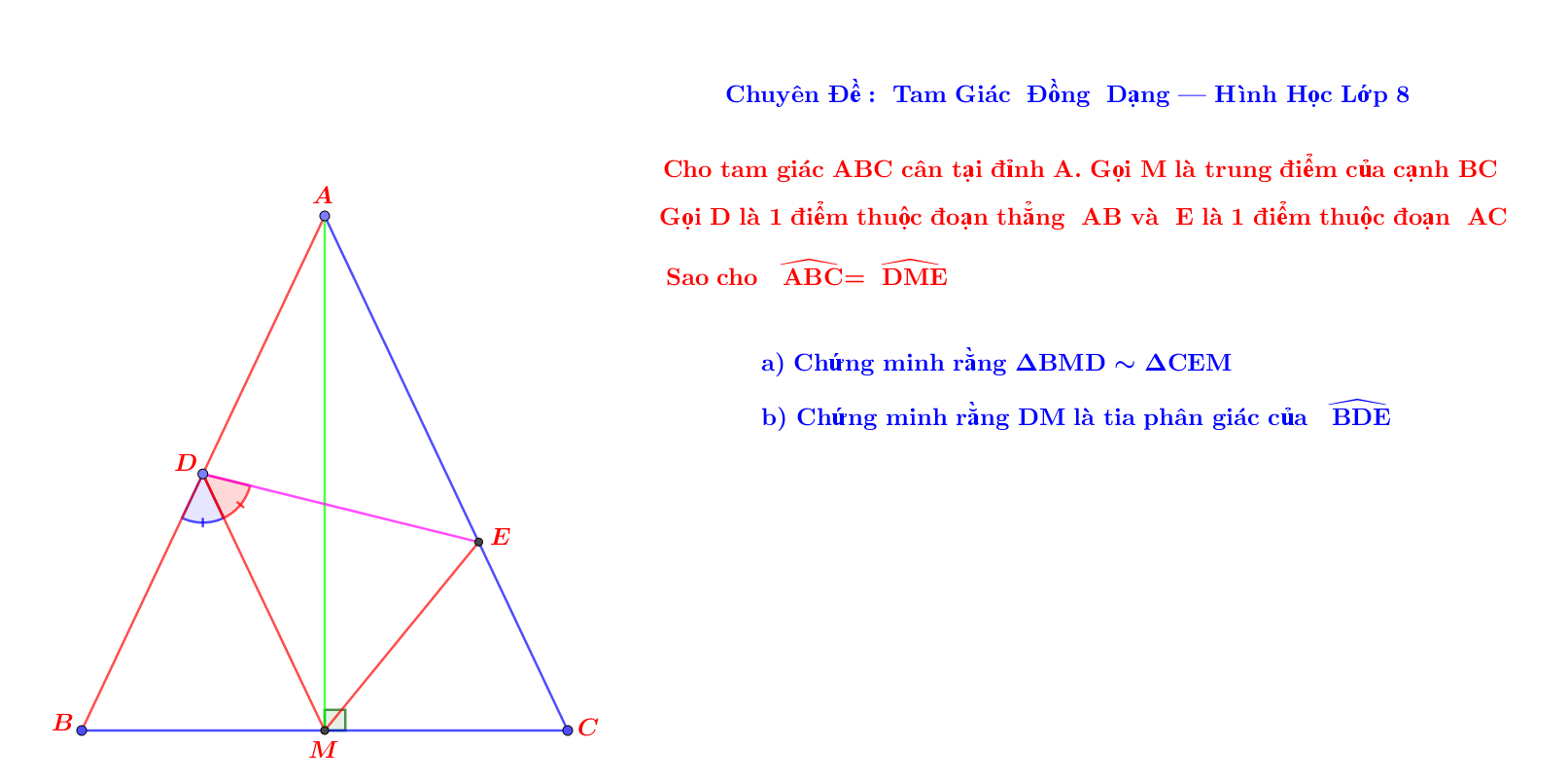
'' Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của đoạn thẳng BC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho \(\widehat{DME}=\widehat{ABC}\)
a) Chứng minh rằng tam giác BMD đồng dạng với tam giác CEM.
b) Chứng minh rằng DM là tia phân giác của góc \(\widehat{BDE}\).
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều ạ!


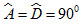
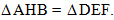
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.
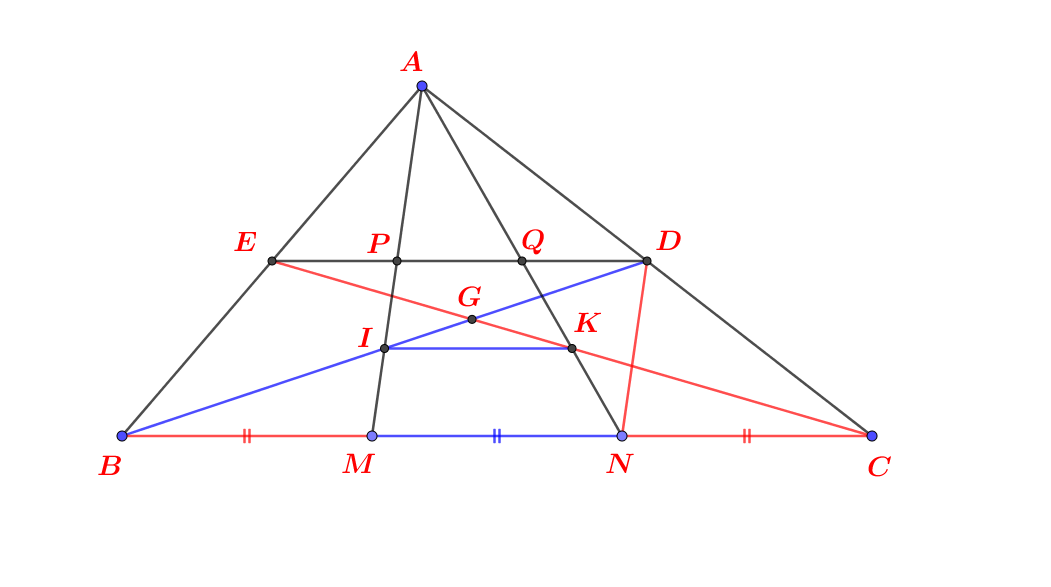
Em xin phép được úp hình học minh họa ạ!