cho tam giác ABC có trung diểm của AH,CI cắt AD tại D vẽ ME song song CD (E thuộc AB)
a) chứng minh AD=DE=EB
b) tính tỉ số Di/DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AD
2 tháng 5 2023
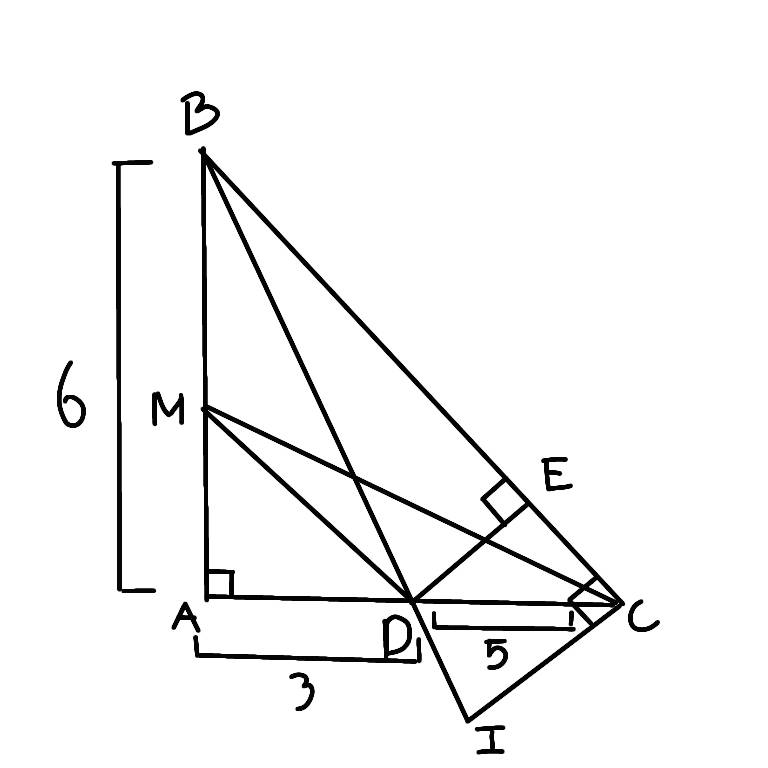a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD
28 tháng 4 2022
Tham khảo
a) Xét 2 tam giác vuông ΔAHB và ΔAHC có:
AH chung
AB = AC (GT)
⇒ Δ AHB = ΔAHC (cạnh huyền - cạnh góc vuông)
b) Ta có : Δ AHB = Δ AHC (câu a)
⇒ ˆBAH=ˆCAHBAH^=CAH^ ( 2 góc tương ứng) (1)
Ta lại có: HD // AC ( GT )
⇒ ˆDHA=ˆCAHDHA^=CAH^ (2 góc so le trong) (2)
Từ (1) và (2) => ˆDHA=ˆBAHDHA^=BAH^
Hay: ˆDHA=ˆDAHDHA^=DAH^
=> ΔADH cân tại D
=> AD = DH
c) Ta có: ΔABH = ΔACH (câu a)
⇔ BH =HC (hai cạnh tương ứng)
⇒ AH là trung tuyến ΔABC tại A ( 3)
Ta có : DH //AC ⇒ ∠DHB = ∠ACB ( 2 góc đồng vị )
Mà ΔABC cân tại A (GT)
⇒ ∠ABC= ∠ACB
⇒ ∠DHB = ∠DBH
=> ΔDHB cân tại D
⇒ DB =DH
Lại có AD = DH (câu b) ⇒ DA=DB
⇒ CD là trung tuyến ΔABC (4)
Từ (3), (4) ta có: AC cắt CD tại G ⇒ G là trọng tâm Δ ABC
Mà CE =EA ⇒ BE là trung tuyến Δ ABC tại B
⇒ BE qua G ⇒ B,G,E thẳng hàng
CM
24 tháng 10 2017
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
16 tháng 3 2022
a: Ta có: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
hay DB=DC
c: Xét ΔKDC có \(\widehat{KDC}=\widehat{KCD}\left(=\widehat{B}\right)\)
nên ΔKDC cân tại K
3 tháng 2 2019
tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go
