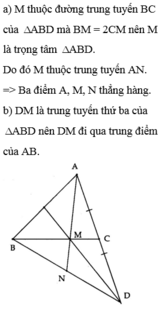
cho ∆ abc. trên cạnh bc lấy điểm m sao cho bm = 2cm. vẽ điểm d sao cho c là trung điểm của ad. gọi n là trung điểm của bd. chứng minh : a, m là trọng tâm của ∆ abd. b, ba điểm a, m, n, thẳng hàng. c, đường thẳng dm đi qua trung điểm của ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2019
Tự vẽ hình
Ta có:
AMB=CMN(2 góc đối đỉnh)
AMC=BMN(2 góc đối đỉnh)
Mà AMB+AMC=180
BMN+MNC=180
=> AMB+BMN=180
=>3 điểm A,M,N thẳng hàng
NH
25 tháng 4 2020
Câu 1:
a, Vì AD là trung tuyến \(\Rightarrow AG=\frac{2}{3}AD\)\(\Rightarrow GD=\frac{1}{3}AD\)\(\Rightarrow GM=\frac{2}{3}AD\)(D là trung điểm MG)
\(\Rightarrow AG=GM\)
Vì BE là trung tuyến \(\Rightarrow BG=\frac{2}{3}BE\)\(\Rightarrow GE=\frac{1}{3}BE\)\(\Rightarrow GN=\frac{2}{3}BE\)(E là trung điểm GN)
\(\Rightarrow BG=GN\)
b, Xét △ANG và △MBG
Có: AG = MG (cmt)
AGN = MGB (2 góc đối đỉnh)
NG = BG (cmt)
=> △ANG = △MBG (c.g.c)
=> AN = MB (2 cạnh tương ứng)
và ANG = MBG (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AN // MB (dhnb)
Câu 2: sai đề???
mong các sư phụ giải đáp hộ e