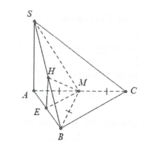
cho hình chóp S.ABC đáy là tam giác cân tại A , cạnh bên SA vuông góc với đáy. M trung điểm BC, J trung điểm BM. Tìm các mp vuông góc mp (ABC)?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương pháp:
Sử dụng quan hệ vuông góc để chứng minh các đáp án và chọn đáp án đúng.
Cách giải:
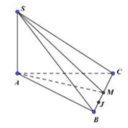
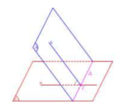
ABC là tam giác cân tại A, M là trung điểm của BC
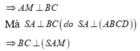
Chọn: C

Chọn C.
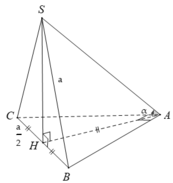
- Gọi H là trung điểm của BC. Suy ra:
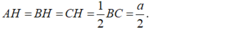
- Ta có:
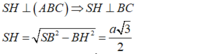
- Do H là hình chiếu của S lên mp(ABC) nên góc giữa đường thẳng SA và mp (ABC) là góc 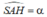
- Xét tam giác vuông SHA có:
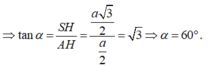

Do \(\Delta ABC\) là tam giác vuông cân và \(BA=BC\) nên \(\Delta ABC\) vuông cân tại \(B \) và \(AC=a\sqrt{2}\).
Trong mp (\(SAB \)) dựng \(AK\perp SB\) với \(K\in SB\)
Trong mp \((SAC)\) dựng \(AH\perp SC\) với \(H\in SC\)
Do \(SA\perp BC\) và \(AB\perp BC\) nên \(BC\perp\left(SAB\right)\)
\(\Rightarrow\) \(\left(SAB\right)\perp\left(SBC\right)\) \(\Rightarrow AK\perp\left(SBC\right)\)
\(\Rightarrow AK\perp SC\) mà \(AH\perp SC\) nên \(SC\perp\left(AHK\right)\)
\(\Rightarrow HK\perp SC\) mà \(\Delta AHK\) vuông tại \(K\) nên góc giữa 2 mp cần tính là \(\widehat{AHK}\)
Áp dụng hệ thức lượng trong tam giác vuông ta tính được \(AH=\dfrac{a\sqrt{2}}{\sqrt{3}}\) và \(AK=\dfrac{a}{\sqrt{2}}\)
\(\Rightarrow\sin\widehat{AHK}=\dfrac{\sqrt{3}}{2}\) \(\Rightarrow\cos\widehat{AHK}=\dfrac{1}{2}\)

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ