Mọi người trình bày cách giải mấy câu này giúp em với...
Đọc tiếp
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!
K
Khách
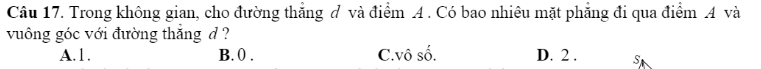
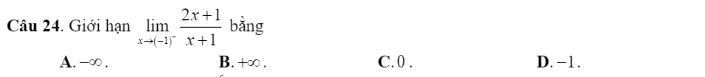
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
2
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
17.
\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(luôn-đúng\right)\\\Delta'=\left(2m-1\right)^2-\left(3m^2-2m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2-2m-3< 0\)
\(\Leftrightarrow-1< m< 3\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
18.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{2\sqrt{5}}{5}\)
\(tan\left(x+\dfrac{\pi}{4}\right)=\dfrac{tanx+tan\dfrac{\pi}{4}}{1-tanx.tan\dfrac{\pi}{4}}=\dfrac{\dfrac{2\sqrt{5}}{5}+1}{1-\dfrac{2\sqrt{5}}{5}.1}=9+4\sqrt{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
19.
\(a^2=b^2+c^2+bc\Rightarrow b^2+c^2-a^2=-bc\)
\(\Rightarrow cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{-bc}{2bc}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)
20.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
\(d\left(I;\Delta\right)=\dfrac{\left|2-1-3\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}IH=d\left(I;\Delta\right)\\AH=\dfrac{1}{2}AB\end{matrix}\right.\)
Áp dụng định lý Pitago trong tam giác vuông IAH:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+AH^2\)
\(\Rightarrow AH=\sqrt{2}\Rightarrow AB=2AH=2\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
12 sai, C mới là đáp án đúng
13 sai, A đúng, \(sin-sin=2cos...sin...\)
18.
\(\Leftrightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=m^2-m\left(-m+3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m^2-3m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< \dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow m=1\)
Đáp án B
22.
Để pt có 2 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1< m< 3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2\left(2m-3\right)}{m-2}\\x_1x_2=\dfrac{5m-6}{m-2}\end{matrix}\right.\)
\(\dfrac{-2\left(2m-3\right)}{m-2}+\dfrac{5m-6}{m-2}\le0\)
\(\Leftrightarrow\dfrac{m}{m-2}\le0\) \(\Leftrightarrow0\le m< 2\)
Kết hợp điều kiện delta \(\Rightarrow1< m< 2\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
24.
Đề bài câu này dính lỗi, ko có điểm M nào cả, chắc là đường thẳng đi qua A
Đường tròn (C) tâm I(1;-2) bán kính R=4
\(\overrightarrow{IA}=\left(1;3\right)\)
Gọi d là đường thẳng qua A và cắt (C) tại 2 điểm B và C. Gọi H là trung điểm BC
\(\Rightarrow IH\perp BC\Rightarrow IH=d\left(I;d\right)\)
Theo định lý đường xiên - đường vuông góc ta luôn có: \(IH\le IA\)
Áp dụng Pitago cho tam giác vuông IBH:
\(BH=\sqrt{IB^2-IH^2}\Leftrightarrow\dfrac{BC}{2}=\sqrt{16-IH^2}\)
\(\Rightarrow BC_{min}\) khi \(IH_{max}\Leftrightarrow IH=IA\)
\(\Leftrightarrow IA\perp d\Rightarrow d\) nhận \(\overrightarrow{IA}\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)
NL
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Câu 10 sai, đáp án B đúng, sử dụng đan dấu trên trục số dễ dàng thấy:
12. Câu này sai, A mới đúng. Đơn giản là em nhìn kĩ lại công thức lượng giác là thấy thôi, nhầm lẫn về hệ số trong công thức biến tích thành tổng
\(cosa.cosb=\dfrac{1}{2}....\)
14. Đáp án C đúng
\(\overrightarrow{BA}=\left(2;2\right)=2\left(1;1\right)\) nên trung trực AB nhận (1;1) là 1 vtpt
Gọi M là trung điểm AB \(\Rightarrow M\left(0;2\right)\)
Phương trình: \(1\left(x-0\right)+1\left(y-2\right)=0\Leftrightarrow x+y-2=0\)
NL
3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C
19 tháng 6 2023
34:
(SBA) giao (SCD)=d đi qua S, d//AB//CD
=>d vuông góc SA,d vuông góc SD
=>(SAB;SCD)=(SA;SD)
tan ASD=AD/AS=1/căn 3
=>góc ASD=30 độ
2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...