Cho 2 tứ giác ABCD VÀ XYZT sao cho 2 Tam giác ABD, XYT đồng dạng. Góc ABC= XYZ và góc ADC= XTZ. Chứng minh Tam giác BCD và YZT đồng dạng Chứng minh góc BAC=YXZ Chứng minh AC/BD= XZ/YT
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


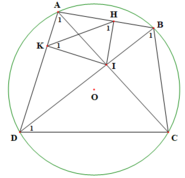
a) Tứ giác AHIK có:
A H I ^ = 90 0 ( I H ⊥ A B ) A K I ^ = 90 0 ( I K ⊥ A D ) ⇒ A H I ^ + A K I ^ = 180 0
=> Tứ giác AHIK nội tiếp.
b) ∆ IAD và ∆ IBC có:
A ^ 1 = B ^ 1 (2 góc nội tiếp cùng chắn cung DC của (O))
A I D ^ = B I C ^ (2 góc đối đỉnh)
=> ∆ IAD ~ ∆ IBC (g.g)
⇒ I A I B = I D I C ⇒ I A . I C = I B . I D
c, Xét đường tròn ngoại tiếp tứ giác AHIK có K ^ 1 = D ^ 1
A ^ 1 = H ^ 1 (2 góc nội tiếp cùng chắn cung IK)
mà A ^ 1 = B ^ 1 ⇒ H ^ 1 = B ^ 1
Chứng minh tương tự, ta được K ^ 1 = D ^ 1
∆ HIK và ∆ BCD có: H ^ 1 = B ^ 1 ; K ^ 1 = D ^ 1
=> ∆ HIK ~ ∆ BCD (g.g)
d) Gọi S1 là diện tích của ∆ BCD.
Vì ∆ HIK ~ ∆ BCD nên:
S ' S 1 = H K 2 B D 2 = H K 2 ( I B + I D ) 2 ≤ H K 2 4 I B . I D = H K 2 4 I A . I C (1)
Vẽ A E ⊥ B D , C F ⊥ B D ⇒ A E / / C F ⇒ C F A E = I C I A
∆ ABD và ∆ BCD có chung cạnh đáy BD nên:
S 1 S = C F A E ⇒ S 1 S = I C I A (2)
Từ (1) và (2) suy ra
S ' S 1 ⋅ S 1 S ≤ H K 2 4 I A . I C ⋅ I C I A ⇔ S ' S ≤ H K 2 4 I A 2 (đpcm)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc EDB=góc ECB

a) Dễ thấy : \(\Delta ABC\) đồng dạng với \(\Delta DEC\) (g.g) (Góc A = Góc CDE; góc C chung)
b) Từ a => \(\frac{AB}{DE}=\frac{AC}{DC}=\frac{BC}{EC}\)
c) Từ b => DC.BC = EC.AC
a: Xét ΔBCD và ΔYZT có
góc DBC=góc TYZ
góc BCD=góc YZT
=>ΔBCD đồng dạng với ΔYZT
b: ΔBCD đồng dạng với ΔYZT
=>góc BDC=góc YTZ
=>góc BAC=góc YXZ