 cau 10 giải chi tiết giúp mình nha
cau 10 giải chi tiết giúp mình nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)
\(=\sqrt{7-2\sqrt{21}+3}+\sqrt{7+2\sqrt{21}+3}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.\sqrt{3}+\left(\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{7}+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{7}-\sqrt{3}\right|+\left|\sqrt{7}+\sqrt{3}\right|\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)
\(=\sqrt{7}+\sqrt{7}=2\sqrt{7}\)
Ta có: \(\sqrt{10-2\sqrt{21}}+\sqrt{10+2\sqrt{21}}\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\)
\(=2\sqrt{7}\)

Ta có :
- 9999=101.99\(\Rightarrow\)999910=(101.99)10=10110.9910
- 9920=9910+10=9910.9910
Vì 10110>9910\(\Leftrightarrow\)10110.9910>9910.9910\(\Leftrightarrow\)999910>9920
Vậy 999910>9920

( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 335 ) x 100
= 2003 x ( 58 + 52 -10 ) + 315 x 100
= 2003 x 100 + 315 x 100
= 200300 + 31500
= 231800
( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 355 ) x 100
= 200300 + 315 x100
= 200300 + 31500
= 231800

( 2003 x 58 + 52 x 2003 - 10 x 2003 ) + ( 670 - 355 ) x 100
= 200300 + 315 x100
= 200300 + 31500
= 231800

Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)


Kẻ OM vuông óc với CD
Vì CD là 1 dây của (O)
=> M là trung điểm của CD
=> MC = MD
Có: AH // BK (cùng vuông góc với CD)
=> AHKB là Hình thang
Lại có: OM vuông góc với CD; O là trung điểm của AB
=> M là trung điểm của HK
=> MH = MK
Có: \(\left\{{}\begin{matrix}HD+MD=HM\\MC+CK=MK\end{matrix}\right.\)
Mà: MH = MK (cmt) và MD = MC (cmt)
=> HD = CK
 Giải giúp mình câu 10 ik giải chi tiết nha
Giải giúp mình câu 10 ik giải chi tiết nha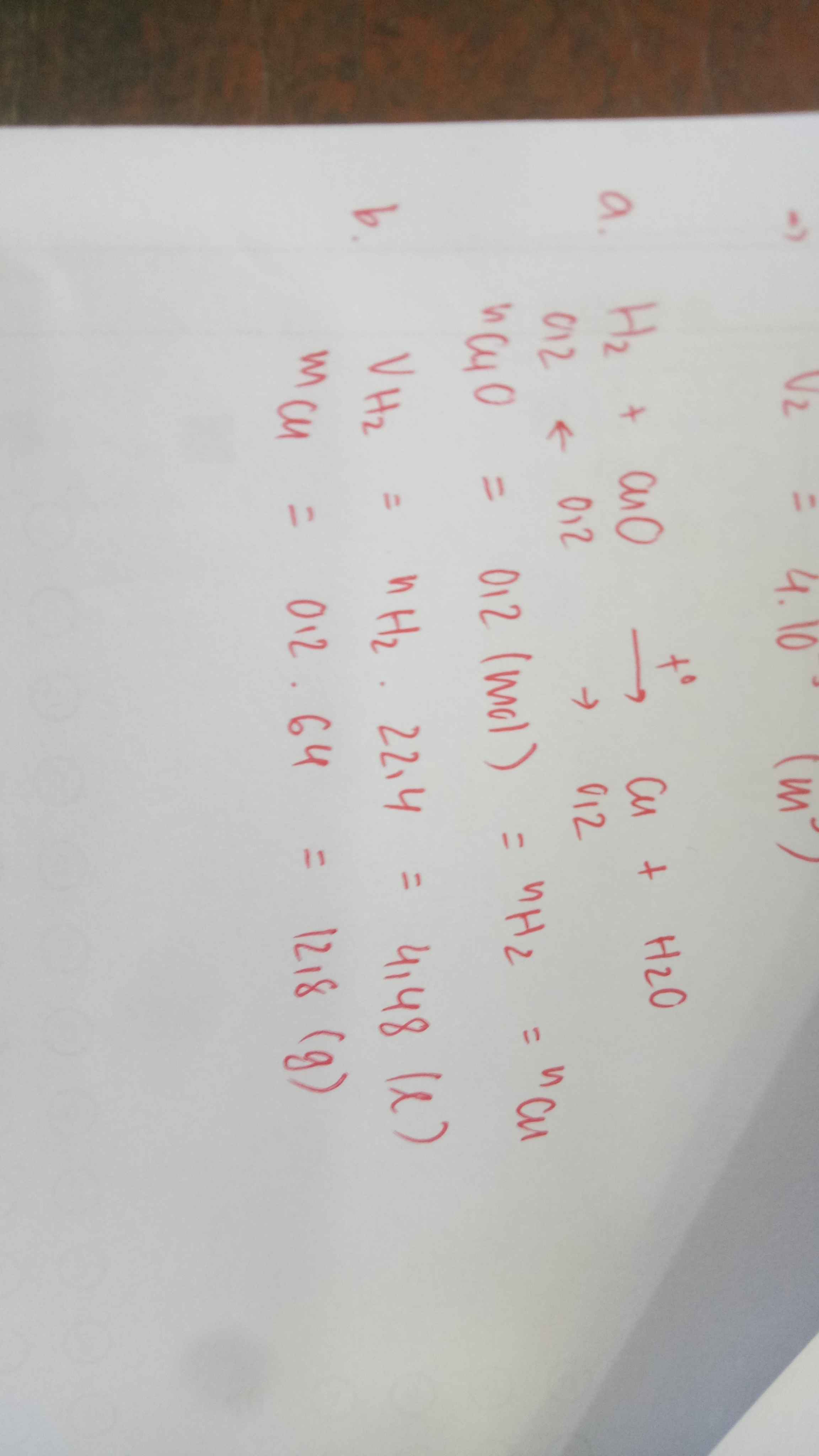

10
\(n_{Zn}=\dfrac{3,25}{65}=0,05\left(mol\right)\)
\(n_{CuO}=\dfrac{6}{80}=0,075\left(mol\right)\)
\(pthh:Zn+HCl->ZnCl_2+H_2\)
0,05 0,05
\(pthh:CuO+H_2\underrightarrow{t^o}H_2O+Cu\)
LTL : \(\dfrac{0,075}{1}>\dfrac{0,05}{1}\)
=>> CuO dư
theo pthh : \(n_{Cu}=n_{H_2}=0,05\)(mol)
=> \(m_{Cu}=0,05.64=3,2\left(g\right)\)
=> \(m_{CuO\left(d\right)}=\left(0,075-0,05\right).80=2\left(g\right)\)
Câu 10:
\(a) n_{Zn} = \dfrac{3,25}{65} = 0,05 (mol)\\n_{CuO} = \dfrac{6}{80} = 0,075 (mol)\)
PTHH:
Zn + 2HCl ---> ZnCl2 + H2
0,05------------------------->0,05
CuO + H2 --to--> Cu + H2O
LTL: \(0,075>0,05\rightarrow\) CuO dư
b, Theo pthh: \(n_{CuO\left(pư\right)}=n_{Cu}=n_{H_2}=0,05\left(mol\right)\)
\(\rightarrow m_{Cu}=0,05.64=3,2\left(g\right)\)
\(c) \text{chất dư là CuO}\\ \rightarrow m_{CuO (dư)} = (0,075 - 0,05) . 80 = 2 (g)\)