Ô tô và xe đạp cùng khởi hành từ A đi B. AB = 60km. Xe đạp có vận tốc 15km/h. Ô tô có vận tốc 60km/h. Giả sử cả hai đều chuyển động thẳng đều. Khi đến B ô tô chuyển động ngược từ B về A sau khi nghỉ ở B 30 phút. Hỏi ô tô và xe đạp gặp nhau cách A bao nhiêu Xem nội dung đầy đủ tạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Gọi t là thời gian đi của ô tô và xe đạp
Quãng đường xe đạp đi được là: \(s_{xđ}=15.t\)
Quãng đường xe ô tô đi từ B về A là:
\(60+60.\left(t-0,5-1\right)\)
\(\Rightarrow\text{}\) \(60+60.\left(t-1,5\right)\)
\(\Rightarrow60.t-30\)
Tổng quãng đường xe đạp và ô tô là:
\(60t-30+15t=60\)
\(\Rightarrow\left\{{}\begin{matrix}75.t=90\\t=1,2h\end{matrix}\right.\)
Như vậy chỗ gặp cách A là:
\(1,2.15=18km\)
Vậy:.............................................................

Một người đi xe đạp với vận tốc 15km/giờ và 1 ô tô đi với vận tốc 45km/giờ, cùng khởi hành lúc 6 giờ sáng từ A để đến B. Lúc 6 giờ 45 phút, một xe máy cũng xuất phát từ A để đến B với vận tốc 35km/h. Hỏi trên đường AB vào lúc mấy giờ thì xe máy ở chính giữa khoảng cách giữa xe đạp và ô tô?

chọn \(Ox\equiv AB,O\equiv A,\) mốc tgian lúc 7h, chiều(+) A->B
\(\Rightarrow\left\{{}\begin{matrix}xA=60t\\xB=120+30t\end{matrix}\right.\)\(\left(km,h\right)\)
gặp nhau \(\Rightarrow xA=xB\Rightarrow t=4h\) gặp nhau lúc 11h
cách B \(S=30.4=120km\)

Chọn đáp án B
? Lời giải:
+ Chọn chiều dương là từ A đến B ,gốc toạ độ tại A, gốc thời gian lúc xe ô tô một khởi hành.
+ Phương trình chuyển động


Chọn đáp án A
![]()
+ Chọn trục Ox cùng phương cùng chiều với AB. Chọn gốc tọa độ trùng với A. Phương trình chuyển động của ô tô: x 1 = 1 2 a t 2 = 0 , 2 t 2
+ Phương trình chuyển động của xe đạp: x 2 = v 0 t + 120 khi hai xe gặp nhau x 1 = x 2 ⇒ 0 , 2 t 2 = v 0 .40 + 120
+ t = 40 s ⇒ 0 , 2. 40 2 = v 0 .40 + 120 ⇒ v 0 = 5 m / s
+ Khoảng ách 2 xe vào thời điểm t = 60s: s = x 1 − x 2 = 0 , 2 t 2 − 5 t − 120 ⇒ s = 0 , 2 60 2 − 5.60 − 120 = 300 n
Vậy vận tốc của xe đạp là 5m/s và khoảng cách giữa hai xe sau thời gian 60s là 300m

Đáp án A
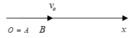
Chọn trục Ox cùng phương cùng chiều với AB. Chọn gốc tọa độ trùng với A. Phương trình chuyển động của ô tô:
x t = 1 2 a t 2 = 0 , 2 t 2
Phương trình chuyển động của xe đạp: x 2 = v 0 t + 120
khi 2 xe gặp nhau
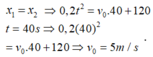
Khoảng cách 2 xe vào thời điểm t=60s:
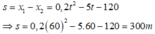
Vậy vận tốc của xe đạp là 5m/s và khoảng cách giữa 2 xe sau thời gian 60s là 300m

Gọi quãng đường AB là s = 60 (km) và vận tốc ô tô, vận tốc xe đạp lần lượt là v1 = 60 và v2 = 15 (km/giờ)
Thời gian ô tô bắt đầu đi từ B về A là: t1 = \(\dfrac{s}{v_1}+\dfrac{1}{2}=\dfrac{60}{60}+\dfrac{1}{2}=\dfrac{3}{2}\)
Trong thời gian t1, xe đạp đi được quãng đường s1 = \(v_2t_1=15.\dfrac{3}{2}=\dfrac{45}{2}\)
Khi ô tô bắt đầu đi từ B về A, hai xe cách nhau s2 = \(s-s_1=60-\dfrac{45}{2}=\dfrac{75}{2}\)
Thời gian để hai xe gặp nhau t2 = \(\dfrac{s_2}{v_1+v_2}=\dfrac{\dfrac{75}{2}}{60+15}=\dfrac{\dfrac{75}{2}}{75}=\dfrac{1}{2}\)
Hai xe gặp nhau chỗ cách A quãng đường s3 = \(60.\dfrac{1}{2}=30\)
Chỗ đó cách B quãng đường s4 = \(s-s_3=60-30=30\)
Vậy...
