Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:
a) Tứ giác BCDE,AECF nội tiếp.
b)góc AFE= ACE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 4 2022
a: Xét tứ giác BCDE có \(\widehat{BCD}+\widehat{BED}=180^0\)
nên BCDE là tứ giác nội tiếp
b: Xét tứ giác AECF có \(\widehat{ACF}=\widehat{FEA}=90^0\)
nên AECF là tứ giác nội tiếp
=>\(\widehat{AFE}=\widehat{ACE}\)
4 tháng 7 2023
a: góc ACB=1/2*sđ cungAB=90 độ
góc DCB+góc DEB=180 độ
=>DEBC nội tiếp
góc AEF=góc ACF=90 độ
=>AECF nội tiếp
b:AECF nội tiếp
=>góc AFE=góc ACE
BH
4 tháng 4 2019
Câu này khá dễ bạn ạ
Tứ giác ABDF nội tiếp vì có BAF+FDB=180 (mà 2 góc đối nhau)
Tứ giác ADCE nội tiếp vì CAE=EDC=90(mà 2 góc cùng nhìn cạnh EC)
ABC=AFE (cùng phụ với BED)
AM là tiếp tuyến nên MAO=90
mà BAC=90 nên BAO=FAM(cùng phụ với OAC)
mặt khác AB=OA=OB=R(gt)
nên tam giác OAB đều mà ABO=MFA,MÀ=BAO nên tam giác AMF đều
22 tháng 6 2022
a: Xét tứ giác BCDE có \(\widehat{DEB}+\widehat{DCB}=180^0\)
nên BCDE là tứ giác nội tiếp
b: Xét tứ giác AECF có \(\widehat{AEF}=\widehat{ACF}=90^0\)
nên AECF là tứ giác nội tiếp
Suy ra: \(\widehat{AFE}=\widehat{ACE}\)
CM
14 tháng 7 2017
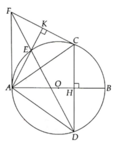
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm
7 tháng 3 2023
a: góc BAC=1/2*sđ cung BC=90 độ
góc BAE+góc EDB=180 độ
=>ABDE nội tiếp
góc CAF=góc CDF=90 độ
=>ADCF nội tiếp
b: góc AEF=góc DEC=90 độ-góc ACB=góc ABC
a: góc ACB=1/2*sđ cung AB=90 độ
góc DCB+góc DEB=180 độ
=>DEBC nội tiếp
góc AEF=góc ACF=90 độ
=>AECF nội tiếp
b: AECF nội tiếp
=>góc AFE=góc ACE