Viếy 1999 số hữu tỉ trên thành 1vòng tròn trong đó tích của 2 số cạnh nhau bằng \(\frac{1}{16}\). Tìm các số đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
0
VT
1
22 tháng 8 2020
Gọi các số hữu tỉ cần tìm là a1,a2,..a1999
Theo bài ra, ta có:
\(a_1.a_2=\frac{1}{9}\)
\(a_2.a_3=\frac{1}{9}\)
..
.
.
\(a_{1998}.a_{1999}=\frac{1}{9}\)
\(\hept{\begin{cases}\frac{a_1.a_2}{a_2.a_3}=1\\\frac{a_2.a_3}{a_3.a_4}=1\\\frac{a_{1997}.a_{1998}}{a_{1998}.a_{1999}}=1\end{cases}}\Rightarrow\hept{\begin{cases}\frac{a_1}{a_3}=1\\\frac{a_2}{a_4}=1\\\frac{a_{1997}}{a_{1999}}=1\end{cases}\Rightarrow\hept{\begin{cases}a_1=a_3\\a_2=a_4\\a_{1997}=a_{1999}\end{cases}}}\Rightarrow a_1=a_2=...=a_{1999}=\frac{1}{3}\)
SoanToiLaCuopGui113
TV
30 tháng 8 2021
gọi 2015 các số đó là : a1,a2,....a2015
theo bài ta có:
a1.a2=a2.a3=....=a2015.a1=1/16 (chú ý : vì các số đó trên 1 vòng tròn nên số đầu liền với số cuối)
suy ra a1=a2=...=a2025
mà a1.a2=a2.a3=....=a2015 suy ra a1.a1=a2.a2=...=a2015.a2015 =1/16
suy ra a1=a2=...=a2025=1/4
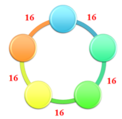
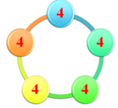
Có:
\(a_1.a_2=\frac{1}{16};a_2.a_3=\frac{1}{16}\Rightarrow a_1=a_3\)
Tương tự như vậy ta có:
Các a???dều bằng nhau hết.
Qua đó ta có chúng thuộc 1 phần 4 hoặc -1 phần 4.
Chúc em học tốt^^