Cho hình chữ nhật ABCD có AB=8cm, BC=6cm và hai đường chéo cắt nhau tại O. Qua B kẻ đường thẳng a vuông góc với BD, a cắt DC tại E.
a) Chứng minh tam giác BCE~tam giác DBE
b) Kẻ đường cao CH của tam giác BCE. Chứng minh BC^2=CH.BD
c) Tính tỉ số diện tích tam giác CEH và diện tích của tam giác DBE
d) Chứng minh 3 đường OE, BC, DH đồng quy


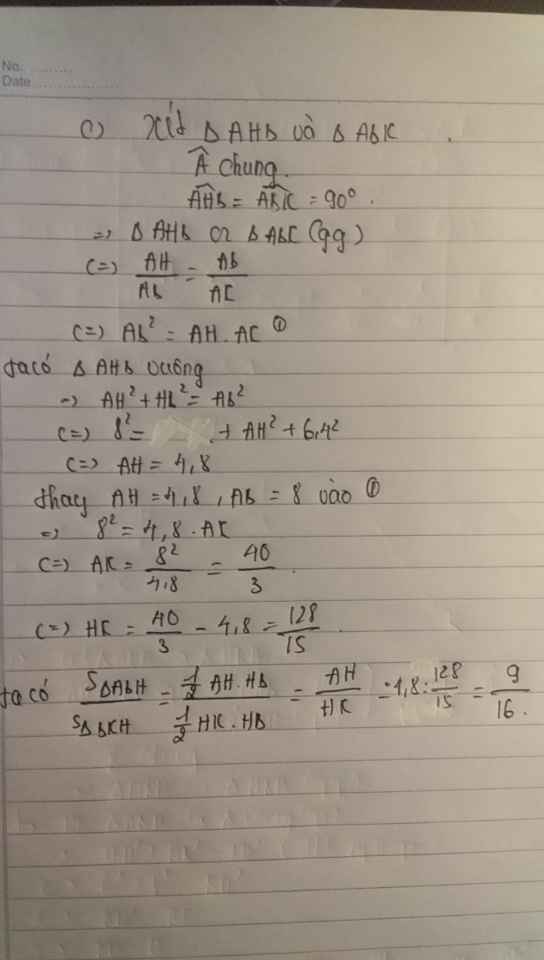
a: Xét ΔBCE vuông tại C và ΔDBE vuông tại B có
góc E chung
=>ΔBCE đồng dạng với ΔDBE
b: Xét ΔCBD vuông tại C và ΔHCB vuông tại H có
góc CBD=góc HCB
=>ΔCBD đồng dạng với ΔHCB
=>CB/HC=BD/CB
=>BC^2=HC*BD
c: CE=6^2/8=4,5cm
CH//DB
=>ΔEHC đồng dạng với ΔEBD
=>S EHC/S EBD=(EC/ED)^2=(4,5/12,5)^2=81/625