Giúp e vẽ hình và giải chi tiết câu 11 ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2022
Câu 17.
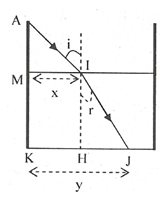
Xét tam giác IHJ vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
Chiết xuất: \(\dfrac{sini}{sinr}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{3}{4}\cdot\dfrac{60^2+HJ^2}{HJ^2}=\dfrac{16}{9}\Rightarrow HJ=51,25cm\)
Độ dài bóng của thành bể tạo ở đáy:
\(HJ+x=85,9cm\)
Chọn A
29 tháng 3 2022
Góc giới hạn phản xạ toàn phần:
\(sini_{gh}=\dfrac{n_2}{n_1}\)
\(\Rightarrow sini_{gh}=\dfrac{\dfrac{4}{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}}{9}\)
\(\Rightarrow i_{gh}=50,2^o\)
Chọn A
29 tháng 3 2022
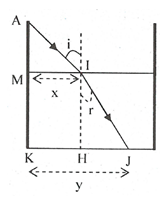
Xét \(\Delta HIJ\) vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
\(\Rightarrow\dfrac{sini}{sinr}=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{60^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow HJ=51,25cm\)
Độ dài vệt sáng:
\(y=x+HJ=85,9cm\)
Chọn B
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
38.
\(y'=2x^2-8x+9=2\left(x-2\right)^2+1\ge1\)
\(\Rightarrow\) Tiếp tuyến có hệ số góc nhỏ nhất bằng 1 khi \(x_0-2=0\Rightarrow x_0=2\)
\(y\left(2\right)=-\dfrac{11}{3}\)
Phương trình d:
\(y=1\left(x-2\right)-\dfrac{11}{3}=x-\dfrac{17}{3}\)
Thay tọa độ 4 điểm của đáp án, chỉ có \(P\left(5;-\dfrac{2}{3}\right)\) thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
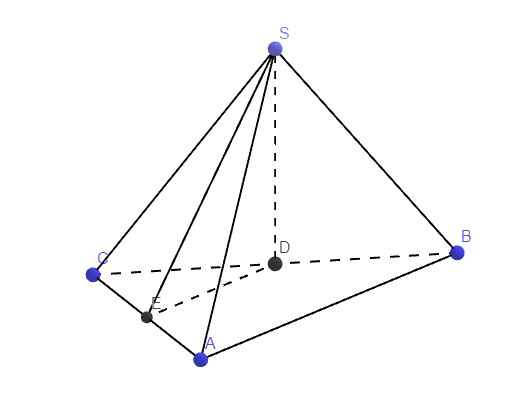
39.
Gọi E là trung điểm AB, F là trung điểm CD
Từ E kẻ EH vuông góc SF (H thuộc SF)
Do tam giác SAB đều \(\Rightarrow SE\perp AB\Rightarrow SE\perp\left(ABCD\right)\)
\(\Rightarrow SE\perp CD\)
\(EF||AD\Rightarrow EF\perp CD\)
\(\Rightarrow CD\perp\left(SEF\right)\) \(\Rightarrow CD\perp EH\)
\(\Rightarrow EH\perp\left(SCD\right)\Rightarrow EH=d\left(E;\left(SCD\right)\right)\)
Lai có: \(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(E;\left(SCD\right)\right)=EH\)
\(SE=\dfrac{AB\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\) ; \(EF=AD=1\)
Hệ thức lượng: \(d=HE=\dfrac{SE.EF}{\sqrt{SE^2+EF^2}}=\dfrac{\sqrt{21}}{7}\)
29 tháng 3 2022
Câu 12.
Ta có: \(\dfrac{sini}{sinr}=n\Rightarrow\dfrac{sin60^o}{sinr}=1,5\)
\(\Rightarrow sinr=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow r\approx35,3^o\)
Chọn C
TN
0
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
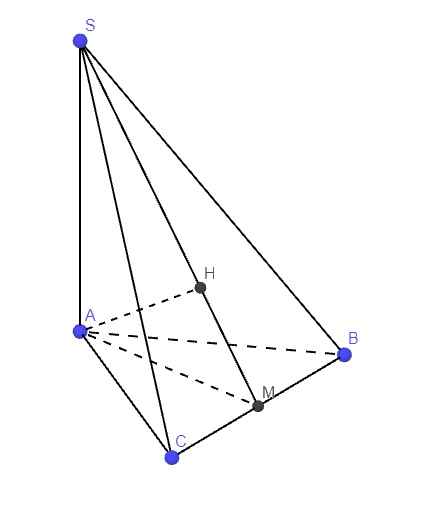
23.
Gọi M là trung điểm BC
Trong mp (SAM), từ A kẻ \(AH\perp SM\) (1)
Ta có: \(AM\perp BC\) (trung tuyến đồng thời là đường cao trong tam giác đều)
Lại có \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAM\right)\Rightarrow BC\perp SH\)
(1);(2) \(\Rightarrow SH\perp\left(SBC\right)\)
\(\Rightarrow SH=d\left(A;\left(SBC\right)\right)\)
\(AM=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Hệ thức lượng trong tam giác vuông SAM:
\(AH=\dfrac{AM.SA}{\sqrt{AM^2+SA^2}}=\dfrac{a\sqrt{66}}{11}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
24.
Gọi D, E lần lượt là trung điểm BC, AC
\(\Rightarrow\) DE là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}DE\perp AC\\DE=\dfrac{1}{2}AB\end{matrix}\right.\)
SBC đều \(\Rightarrow SD\perp BC\Rightarrow SD\perp\left(ABC\right)\)
\(\Rightarrow SD\perp AC\)
\(\Rightarrow AC\perp\left(SDE\right)\Rightarrow\widehat{SED}\) là góc giữa (SAC) và (ABC)
\(AB=BC.cos\widehat{ABC}=a.cos30^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow DE=\dfrac{1}{2}AB=\dfrac{a\sqrt{3}}{4}\)
\(SD=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(tan\varphi=tan\widehat{SED}=\dfrac{SD}{DE}=2\)
giải giúp e câu 4,5 có hình và lời giải chi tiết ạ !
Chiết suất tuyệt đối của kim cương:
Áp dụng công thức: \(n=\dfrac{c}{v}\)
\(\Rightarrow\)Tôc độ truyền ánh sáng trong kim cương:
\(v=\dfrac{c}{n}=\dfrac{3\cdot10^8}{2,42}=1,24\cdot10^8\)m/s=124000km/h
Chọn B.