Rút gọn biểu thức: A=1+1/2+1/22+1/23+...+1/22012
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
NT
27 tháng 4 2021
a.Chứng tỏ rằng B = 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + 1/72 +1/82 < 1
b.Cho S = 3/1.4 + 3/4.7 + 3/7.10 +......+3/40.43 + 3/43.46 hãy chứng tỏ rằng S < 1
NT
27 tháng 4 2021
Xin lỗi mọi người mình tính đặt câu hỏi nhưng ấn nhầm phần trả lời ạ!
NG
1
26 tháng 8 2021
\(S=1-2+2^2-2^3+...+2^{2012}-2^{2013}\)
\(\Rightarrow2S=2-2^2+2^3-2^4+...+2^{2013}-2^{2014}\)
\(\Rightarrow2S+S=2-2^2+2^3-...-2^{2014}+1-2^2-2^3+...-2^{2013}\)
\(\Rightarrow3S=1-2^{2014}\)\(\Rightarrow3S-2^{2014}=1-2^{2015}\)
ID
12 tháng 5 2022
Đặt N = 1 + 2 + 22 +...+ 22012
2N = 2 + 22 + 23 +...+ 22013
2N - N = (2 + 22 + 23+....+ 22013) - (1 + 2 + 22 +....+ 22012)
N = 22013 - 1
Thay N vào M ta được:
\(M=\dfrac{2^{2013}-1}{2^{2014}-2}=\dfrac{2^{2013}-1}{2\left(2^{2013}-1\right)}=\dfrac{1}{2}\)
BC
12 tháng 5 2022
Đặt \(N=1+2+2^2+...+2^{2012}\)
\(2N=2+2^2+2^3+...+2^{2013}\)
\(2N-N=\left(2+2^2+2^3+...+2^{2013}\right)-\left(1+2+2^2+...+2^{2012}\right)\)
\(N=2^{2013}-1\)
Thay N vào M ta được:
\(M=\dfrac{2^{2013-1}}{2^{2014}-2}=\dfrac{2^{2013}-1}{2\left(2^{2013}-1\right)}=\dfrac{1}{2}\)
CM
3 tháng 9 2017
A = 3 − 1 + 3 + 1 ( 3 + 1 ) ( 3 − 1 ) + 2 ( 2 − 3 ) 2 = 2 3 3 − 1 + 2 − 3 = 3 + 2 − 3 = 2
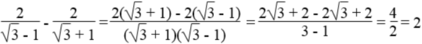
A= 1+ 1/2 + 1/22 + ... + 1/22012
(1/2)A= 1/2+1/22+...+1/22013
A-(1/2)A= (1+ 1/2 + 1/22 + ... + 1/22012) - ( 1/2+1/22+...+1/22013)
(1/2)A = 1 - 1/22013
A= (1- 1/22013) : 1/2
A= 2 - 1/22012