Có hai bình nhiệt lượng kế, bình I chứa m 1 = 2kg nước ở nhiệt độ t 1 = 30 0 C, bình II chứa m 2 (kg) nước ở nhiệt độ t 2 ( 0 C). Người ta đổ thêm một lượng nước m 3 = 1 kg ở nhiệt độ t 3 = 90 0 C vào bình I.
a) Tính nhiệt độ của nước trong bình I sau khi cân bằng nhiệt;
b) Nếu đổ một nửa nước trong bình II sang bình I thì nhiệt độ của nước sau khi cân bằng nhiệt là 42,5 0 C. Nếu đổ toàn bộ nước trong bình II sang bình I thì nhiệt độ của nước sau khi cân bằng nhiệt là 38 0 C. Tính m 2 , t 2 .
Cho nhiệt dung riêng của nước là 4200J/kg.K. Bỏ qua sự trao đổi nhiệt giữa nước với bình và với môi trường ngoài.
mik cần gấp, mong các bn giúp
help me!!!!


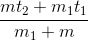 (1)
(1) 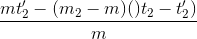 (2)
(2)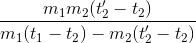 =
=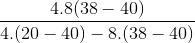 =1kg
=1kg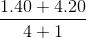 = 24
= 24