Cho ABC vuông tại A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là giao điểm của BH và CA. Chứng minh rằng:
a) BE = BD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

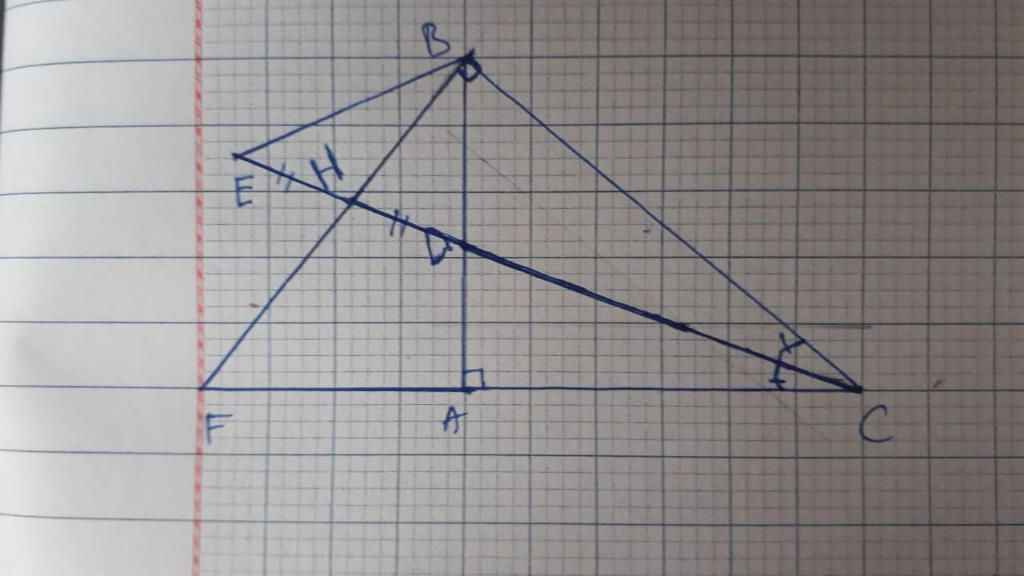
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE

a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE

a) Ta có : \(∠ C E B = ∠ A D C\)
\(E H = D H\)
\(BH\) chung
\(Δ E B H = Δ D B H\)
\(∠ E B H = ∠ D B H \)
\(BF\) là tia phân giác \(∠ B\)
b) Chứng minh được \(∠ B E D = ∠ A D C\)
\(F B A = F C D\)
Bạn có thể làm câu b và c rõ ràng 1 tí được khum ạ. Mik rất cảm ơn bn!

a: Xét ΔBHE vuông tại H và ΔBHD vuông tại H có
HB chung
HE=HD
DO đó: ΔBHE=ΔBHD
Suy ra: \(\widehat{EBH}=\widehat{DBH}\)
hay BF là phân giác của góc EBD
b: \(\widehat{FBA}+\widehat{F}=90^0\)
\(\widehat{FCH}+\widehat{F}=90^0\)
Do đó: \(\widehat{FBA}=\widehat{FCH}\)

a) Xét tam giác BHE vuông góc tại H và tam giác BHD vuông góc tại H:
HE = HD (H là trung điểm ED).
BD chung.
\(\Rightarrow\) Tam giác BHE = Tam giác BHD (cạnh huyền - góc nhọn).
\(\Rightarrow\) \(\widehat{EBH}=\widehat{DBH}\) (2 góc tương ứng).
\(\Rightarrow\) BH là phân giác \(\widehat{EBD}.\)
\(\Rightarrow\) BF là phân giác \(\widehat{EBD}.\)
b) Xét tam giác CAD: \(\widehat{CAD}+\widehat{CDA}+\widehat{ACD}=180^o\) (Tổng 3 góc trong tam giác).
Xét tam giác BHD: \(\widehat{BHD}+\widehat{BDH}+\widehat{HBD}=180^o\) (Tổng 3 góc trong tam giác).
Mà \(\widehat{CAD}=\widehat{BHD}\left(=90^o\right);\widehat{CDA}=\widehat{BDH}\) (đối đỉnh).
\(\Rightarrow\widehat{ACD}=\widehat{HBD}.\\ \Rightarrow\widehat{FCH}=\widehat{FBA}.\)
b) CMR FBA=FCH