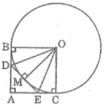
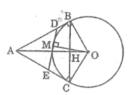
Cho đường tròn tâm O và hai điểm B,C thuộc đường tròn . Các tiếp tuyến của đường tròn tại B và C cắt nhau tại A. M là 1 điểm thuộc cung nhỏ BC. Tiếp tuyến của đường tròn tại M cắt AB,AC theo thứ tự ở D và E . BC cắt OD ở I và cắt OE tại K. Chứng minh rằng:
a, DB.DE=DI.DO
b,OM,DK,EI đồng quy.