mọi người giải giúp mình được khộng ạ ? mình cảm ơn rất nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
SN
1
Những câu hỏi liên quan
14 tháng 12 2021
\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
14 tháng 12 2021
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...
NN
1
NK
0
12 tháng 3 2022
Bài 1 :
Thay x = 2 ; y = -1/2 ta được
\(B=-8+2.4\left(-\dfrac{1}{2}\right)-4.2.\left(\dfrac{1}{4}\right)+2\left(-\dfrac{1}{2}\right)-3\)
\(=-8-4-2-1-3=-18\)
6 tháng 2 2021
a) Ta có: \(\left(2x-3\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};-\dfrac{4}{3}\right\}\)
b) Ta có: \(x^3-3x^2+3x-1=\left(x-1\right)\left(x+1\right)\)
\(\Leftrightarrow\left(x-1\right)^3-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2-2x+1-x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-3x\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=3\end{matrix}\right.\)
Vậy: S={0;1;3}
c) Ta có: \(x^2+x=2x+2\)
\(\Leftrightarrow x\left(x+1\right)-2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Vậy: S={-1;2}
d) Ta có: \(\left(x-1\right)^2=2\left(x^2-1\right)\)
\(\Leftrightarrow\left(x-1\right)^2-2\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-1-2x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)Vậy: S={1;-3}
e) Ta có: \(2\left(x+2\right)^2-x^3-8=0\)
\(\Leftrightarrow2\left(x+2\right)^2-\left(x^3+8\right)=0\)
\(\Leftrightarrow2\left(x+2\right)\cdot\left(x+2\right)-\left(x+2\right)\left(x^2-2x+4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x+4-x^2+2x-4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\cdot\left(-x^2+4x\right)=0\)
\(\Leftrightarrow-x\left(x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=4\end{matrix}\right.\)
Vậy: S={0;-2;4}
31 tháng 10 2021
a: \(P=-\left|5-x\right|+2019\le2019\forall x\)
Dấu '=' xảy ra khi x=5
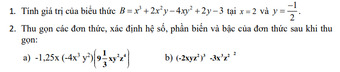
Câu 2:
\(TH1:m+2=0. \Leftrightarrow m=-2.\)
Thay \(m=-2\) vào BPT ta có:
\(0x+\left(-2\right)^2-3>0.\\ \Leftrightarrow4-3>0.\)
\(\Leftrightarrow1>0\) (Luôn đúng).
Vậy \(m=-2\) thì BPT có nghiệm.
\(TH2:m+2\ne0.\Leftrightarrow m\ne-2.\)
Khi đó BPT có nghiệm \(x>\dfrac{3-m^2}{m+2}.\)
Vậy bất phương trình có nghiệm với mọi giá trị thực của m.