Có ai ko giúp mik voi mik cần gấp .cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


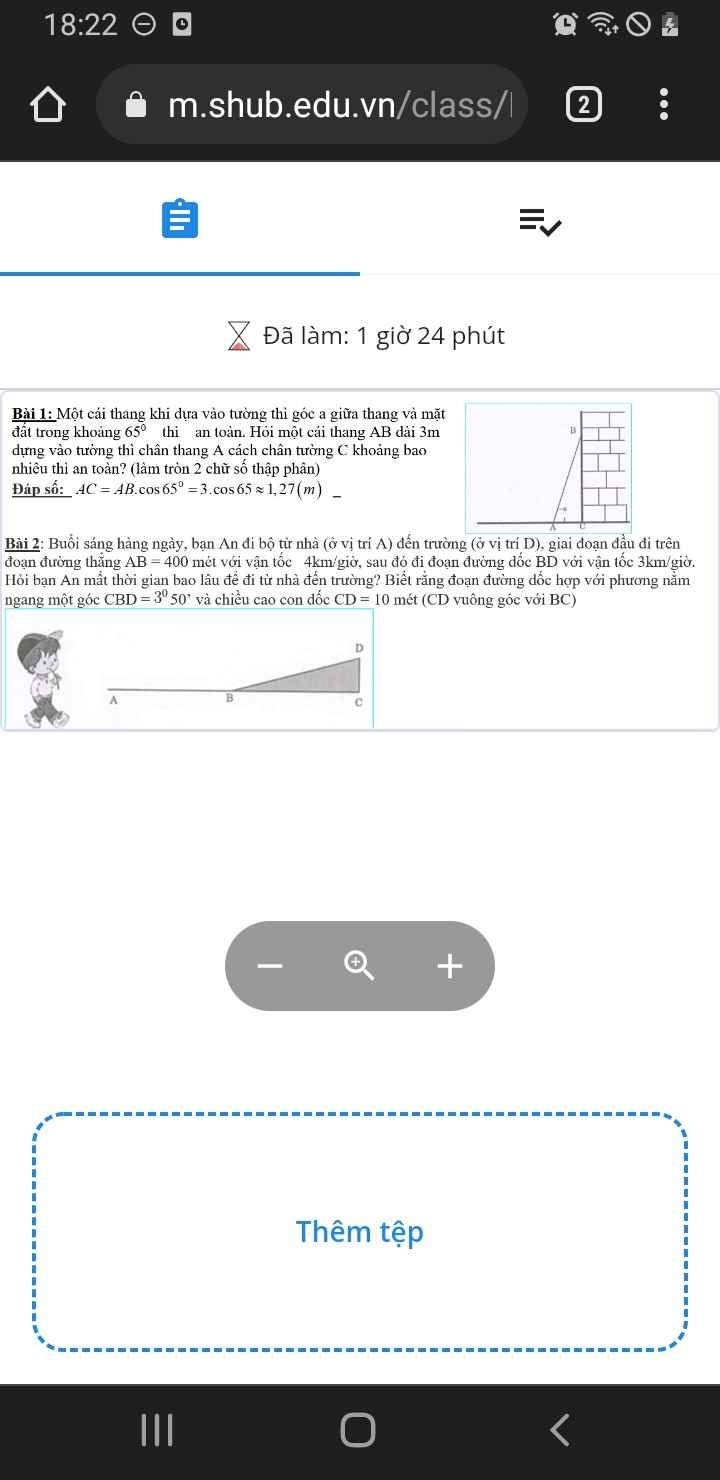
Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)

c: \(=\dfrac{-27\cdot100}{-30}=\dfrac{2700}{30}=90\)

a: =>x>=0 và x^2+x=x^2
=>x=0
a: =>x>=1 và 1-x^2=x^2-2x+1
=>-2x^2+2x=0 và x>=1
=>x=1
a: =>x>=1 và 1-2x^2=x^2-2x+1
=>-3x^2+2x=0 và x>=1
=>\(x\in\varnothing\)
a: ĐKXĐ: x<=2 và x^2-2x=x^2-4x+4
=>x=2
a: =>căn x^2-4=x-2
=>x>=2 và x^2-4=x^2-4x+4
=>x>=2 và 4x=8
=>x=2
b: =>x>=0 và x^2-4x+1=x^2
=>-4x+1=0 và x>=0
=>x=1/4
b: =>x>=-1 và x^2+x+1=x^2+2x+1
=>x=0
c: =>x>=1 và 4x^2-8x+1=x^2-2x+1
=>x>=1 và 3x^2-6x=0
=>x=2
b: =>x>=-1 và 5x^2-2x+2=x^2+2x+1
=>x>=-1 và 4x^2-4x+1=0
=>x=1/2
b: =>căn 4x^2-x+1=2x+3
=>x>=-3/2 và 4x^2-x+1=(2x+3)^2=4x^2+12x+9
=>x>=-3/2 và -13x=8
=>x=-8/13

\(a,\dfrac{11x}{2x-5}+\dfrac{x-30}{2x-5}=\dfrac{11x+x-30}{2x-5}=\dfrac{12x-30}{2x-5}=\dfrac{6\left(2x-5\right)}{2x-5}=6\)
\(b,\dfrac{3x^2-1}{2x}+\dfrac{x^2+1}{2x}=\dfrac{3x^2-1+x^2+1}{2x}=\dfrac{4x^2}{2x}=2x\)
\(c,\dfrac{3}{2x-5}+\dfrac{-2}{2x+5}+\dfrac{-20}{4x^2-25}=\dfrac{3\left(2x+5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{2\left(2x-5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{6x+15-4x+10-20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{2x+5}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{1}{2x-5}\)
\(d,\dfrac{x-2}{x-1}+\dfrac{x-3}{x+1}+\dfrac{4-2x^2}{x^2-1}=\dfrac{\left(x-2\right)\left(x+1\right)+\left(x-3\right)\left(x-1\right)+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+x-2+x^2-3x-x+3+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5}{x-1}\)
\(e,\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}+\dfrac{4}{x^2-1}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1-x^2+2x-1+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)


2:
a: AC=căn 5^2-3^2=4cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4
b: AB=căn 13^2-12^2=5cm
sin B=AC/BC=12/13
cos B=AB/BC=5/13
tan B=12/13:5/13=12/5
cot C=1:12/5=5/12
c: BC=căn 4^2+3^2=5cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4




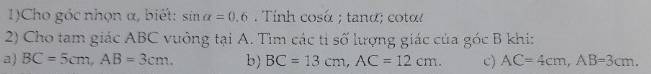
#include <bits/stdc++.h>
using namespace std;
int n,i,x,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x%2==0) dem++;
}
cout<<dem;
return 0;
}