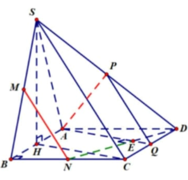
Chóp SABCD đáy là hình vuông cạnh a tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy m,n,p là trung điểm bc,sd,sb.Tính d(mn,ap)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 11 2017
Chọn B.
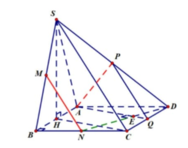
Gọi Q là trung điểm CD, ta có PQ//SC//MN nên MN//(APQ)
=> d(MN, PQ)=d(MN, (APQ))=d(N,(APQ))
Vì N D ⊥ H C N D ⊥ S H ⇒ N D ⊥ ( S H C )
⇒ N D ⊥ S C ⇒ N D ⊥ P Q
A Q → . N D → = ( A D → + D Q → ) . ( D C → + C N → ) = 0 → ⇒ A Q ⊥ N D
Vậy có
N D ⊥ P Q N D ⊥ A Q ⇒ N D ⊥ A P Q t ạ i E ⇒ d ( M N , A P ) = N E
Mà có
1 D E 2 = 1 D A 2 + 1 D Q 2 = 5 a 2 ⇒ D E = a 5
Và D N = a 5 2 ⇒ E N = 3 a 5 10
Vậy d ( M N , A P ) = 2 a 10
CM
30 tháng 9 2019
Đáp án C.
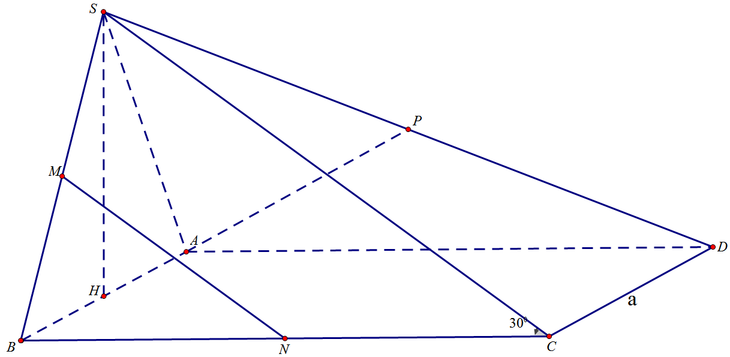
Trong không gian Oxyz:
Chọn A ≡ O 0 ; 0 ; 0 ; B a ; 0 ; 0 ; D 0 ; a ; 0 ; C a ; a ; 0
⇒ H a 2 ; 0 ; 0 ; S a 2 ; 0 ; a 3 2 ; M 3 a 4 ; 0 ; a 3 4 ; N a ; a 2 ; 0 ; P a 4 ; a 2 ; a 3 4
Ta có:
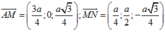
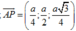
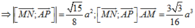
⇒ d M N ; A P = M N → ; A P → . A M → M N → ; A P → = 3 5 10 a
CM
2 tháng 12 2018
Chọn B
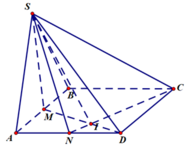
Ta có:
Do tam giác SAB đều => SM vuông góc với AB
Mà (SAB) vuông góc với mặt phẳng đáy => SM chính là đường cao của khối chóp SABCD
Mà SM vuông góc với NC ( Do SM vuông góc với đáy ABCD)
=> NC vuông góc với (SMD)
=> SI vuông góc với NC
CM
30 tháng 4 2019
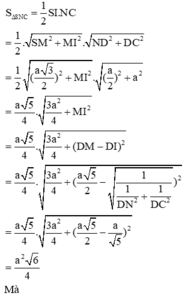
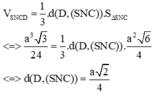
Đáp án là C
ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊥ A B ⇒ S H ⊥ A B C D
mà D I ⊥ C H D I ⊥ S H ⇒ D I ⊥ S H C ⇒ d D , S H C = D I = 2 a 2
ta có
Δ B H C = Δ A H E ⇒ S Δ B H C = S Δ A H E ; H E = H C
mà
S A B C D = S A H C D + S Δ B H C = S A H C D + S Δ A H E = S Δ D C E
Tam giác SAB đều nên . S H = a 3
Tam giác SHC có
H C = S C 2 − S H 2 = a 2 ⇒ E C = 2 H C = 2 a 2 .
Khi đó S A B C D = S Δ D C E = 1 2 D I . E C = 4 a 2 .
Vậy V A B C D = 1 3 S H . S A B C D = 1 3 a 3 .4 a 2 = 4 a 3 3 3 .
CM
31 tháng 3 2018
Chọn đáp án C
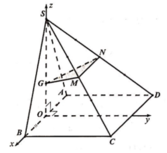
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: 
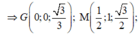
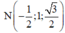
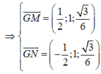
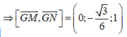
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là 
Mặt phẳng (GMN) có vecto pháp tuyến là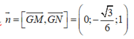 
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
CM
11 tháng 8 2019
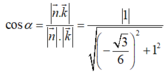
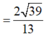
Chọn đáp án C
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên S O ⊥ A B C D
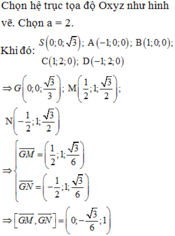
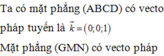
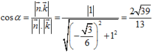
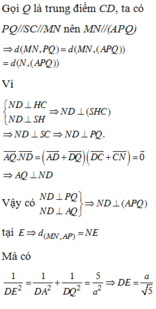
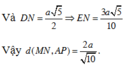
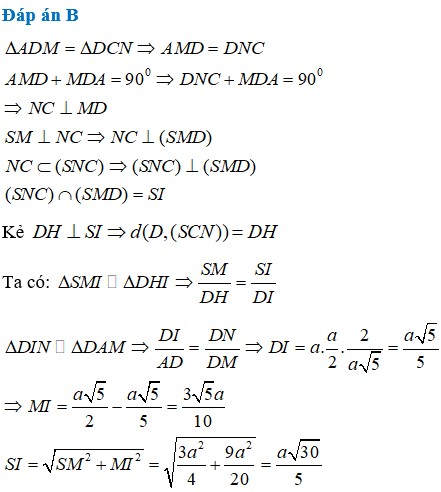
lỗi hình r ạ
lx