Cho đường tròn (C) x^2 + y^2 - 6x - 2y + 1 = 0.
Viết phường trình đường thẳng đi qua M(0;2) và cắt (C) theo một dây cung có độ dài bằng 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 11 2019
Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
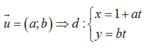
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
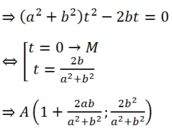
- Nếu d cắt (C2) tại B:
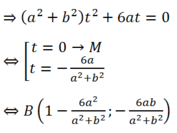
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 3 2023
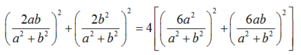
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\sqrt{5}\)
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;\Delta\right)\)
\(S_{IAB}=\dfrac{1}{2}IH.AB=\dfrac{1}{2}IH.2AH=IH.\sqrt{IA^2-IH^2}=IH.\sqrt{20-IH^2}\)
\(\Rightarrow IH\sqrt{20-IH^2}=8\)
\(\Rightarrow IH^4-20IH^2+64=0\Rightarrow\left[{}\begin{matrix}IH=4\\IH=2\end{matrix}\right.\)
\(\overrightarrow{IM}=\left(-1;-2\right)\Rightarrow IM=\sqrt{5}\), mà \(IH\le IM\Rightarrow IH=2\)
Gọi \(\left(a;b\right)\) là 1 vtpt của \(\Delta\) với a;b không đồng thời bằng 0
\(\Rightarrow\) Phương trình \(\Delta\): \(a\left(x-1\right)+b\left(y+3\right)=0\Leftrightarrow ax+by-a+3b=0\)
\(d\left(I;\Delta\right)=IH\Leftrightarrow\dfrac{\left|2a-b-a+3b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+2b\right|=2\sqrt{a^2+b^2}\)
\(\Leftrightarrow a^2+4ab+4b^2=4a^2+4b^2\)
\(\Rightarrow3a^2-4ab=0\Rightarrow\left[{}\begin{matrix}a=0\\3a=4b\end{matrix}\right.\)
Chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(0;1\right)\\\left(a;b\right)=\left(4;3\right)\end{matrix}\right.\) \(\Rightarrow\) có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y+3=0\\4x+3y+5=0\end{matrix}\right.\)
CM
12 tháng 11 2019
Đáp án A
Đường tròn (C) có tâm 
Do đó:
ở trong đường tròn.
Để A là trung điểm của 
là vectơ pháp tuyến của d nên d có phương trình: -1 (x+ 4) + 1.( y-2) =0
Hay x- y + 6= 0.
