Giup em với mng ạ. em cảm ơn.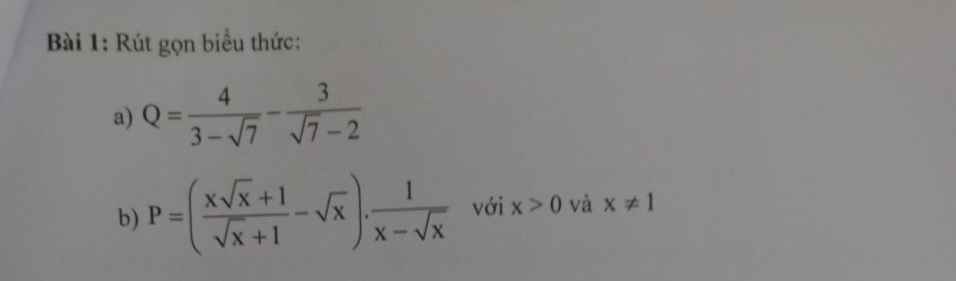
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
11 tháng 4 2022
Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5
HP
12 tháng 4 2021
Gọi nhiệt độ cân bằng là \(t\left(t_2< t< t_3\right)\)
Giả sử \(t>t_1\Rightarrow Q_{thu}=Q_1+Q_2;Q_{tỏa}=Q_3\)
\(Q_{thu}=Q_{tỏa}\)
\(\Leftrightarrow Q_1+Q_2=Q_3\)
\(\Leftrightarrow m_1.C_1.\left(t-t_1\right)+m_2.C_2.\left(t-t_2\right)=m_3.C_3.\left(t_3-t\right)\)
\(\Leftrightarrow2000.\left(t-6\right)+10.4000.\left(t+40\right)=5.2000.\left(60-t\right)\)
\(\Leftrightarrow t=-19^oC\) (Trái với giả sử)
\(\Rightarrow t< t_1\Rightarrow Q_{thu}=Q_2;Q_{tỏa}=Q_1+Q_3\)
\(Q_{thu}=Q_{tỏa}\)
\(\Leftrightarrow m_2.C_2.\left(t-t_2\right)=m_1.C_1.\left(t-t_1\right)+m_3.C_3.\left(t_3-t\right)\)
\(\Leftrightarrow10.4000.\left(t+40\right)=2000.\left(t-6\right)+5.2000.\left(60-t\right)\)
\(\Leftrightarrow t=-19^oC\)
Kết luận: Nhiệt độ khi cân bằng là \(t=-19^oC\)
HN
7 tháng 11 2021
Bài 1: a) 0,36AA : 0,48Aa : 0,16aa.
b) A = 0,6 và a = 0,4.
Bài 2: Quần thể đang ở trạng thái cân bằng, suy ra tần số alen cần tìm a = 0,4 và A = 0,6.
Bài 3: QT1 đạt trạng thái cân bằng di truyền do \(\sqrt{0,36}+\sqrt{0,16}=1\).
QT2 chưa đạt trạng thái cân bằng đi truyền do \(\sqrt{0,7}+\sqrt{0,1}\ne1\).
Bài 4: Tần số alen của quần thể là A = \(\dfrac{40.2}{\left(40+20+40\right).2}+\dfrac{20}{\left(40+20+40\right).2}=0,5\) và a = 0,5.
Quần thể đã nêu không đạt trạng thái cân bằng về thành phần kiểu gen do \(\sqrt{\dfrac{40}{40+20+40}}+\sqrt{\dfrac{40}{40+20+40}}\ne1\).
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2022
\(\lim\limits_{x\rightarrow-\infty}\dfrac{3x^3-5x-6}{1-4x^3+x^2}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^3\left(3-\dfrac{5}{x^2}-\dfrac{6}{x^3}\right)}{x^3\left(\dfrac{1}{x^3}-4+\dfrac{1}{x}\right)}=\lim\limits_{x\rightarrow-\infty}\dfrac{3-\dfrac{5}{x^2}-\dfrac{6}{x^3}}{\dfrac{1}{x^3}-4+\dfrac{1}{x}}=\dfrac{3-0-0}{0-4+0}=-\dfrac{3}{4}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(3x^2+8\right)\left(2x+1\right)}{5-4x^3}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(3+\dfrac{8}{x}\right)x\left(2+\dfrac{1}{x}\right)}{x^3\left(\dfrac{5}{x^3}-4\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(3+\dfrac{8}{x}\right)\left(2+\dfrac{1}{x}\right)}{\dfrac{5}{x^3}-4}=\dfrac{\left(3+0\right)\left(2+0\right)}{0-4}=-\dfrac{6}{4}=-\dfrac{3}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2022
\(\lim\limits_{x\rightarrow+\infty}\dfrac{-5x+7}{3-2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{x\left(-5+\dfrac{7}{x}\right)}{x\left(\dfrac{3}{x}-2\right)}=\lim\limits_{x\rightarrow+\infty}\dfrac{-5+\dfrac{7}{x}}{\dfrac{3}{x}-2}=\dfrac{-5+0}{0-2}=\dfrac{5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{7}{2x-1}=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{7}{x}}{2-\dfrac{1}{x}}=\dfrac{0}{2-0}=0\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 2 2021
a.
C là trung điểm của AD nên tọa độ D thỏa mãn:
\(\left\{{}\begin{matrix}x_D=2x_C-x_A=-3\\y_D=2y_C-y_A=3\\z_D=2z_C-z_A=4\end{matrix}\right.\) \(\Rightarrow D\left(-3;3;4\right)\)
b.
Gọi \(E\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3;0;-3\right)\\\overrightarrow{EC}=\left(-2-x;2-y;3-z\right)\end{matrix}\right.\)
ABCE là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2-x=3\\2-y=0\\3-z=-3\end{matrix}\right.\) \(\Leftrightarrow E\left(-5;2;6\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 2 2021
c.
Gọi \(F\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{FA}=\left(-1-x;1-y;2-z\right)\\\overrightarrow{FB}=\left(2-x;1-y;-1-z\right)\\\overrightarrow{FC}=\left(-2-x;2-y;3-z\right)\end{matrix}\right.\)
\(2\overrightarrow{FA}+3\overrightarrow{FB}=\overrightarrow{FC}\Leftrightarrow\left\{{}\begin{matrix}2\left(-1-x\right)+3\left(2-x\right)=-2-x\\2\left(1-y\right)+3\left(1-y\right)=2-y\\2\left(2-z\right)+3\left(-1-z\right)=3-z\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{4}\\z=-\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow F\left(\dfrac{3}{2};\dfrac{3}{4};-\dfrac{1}{2}\right)\)
d.
Gọi G có tọa độ dạng: \(G\left(x;y;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AG}=\left(x+1;y-1;-2\right)\\\overrightarrow{BG}=\left(x-2;y-1;1\right)\end{matrix}\right.\)
Ba điểm A;B;G thẳng hàng khi:
\(\dfrac{x-2}{x+1}=\dfrac{y-1}{y-1}=\dfrac{1}{-2}\)
\(\Rightarrow\) Không tồn tại G thỏa mãn yêu cầu đề bài
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.
29 tháng 5 2022
Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh
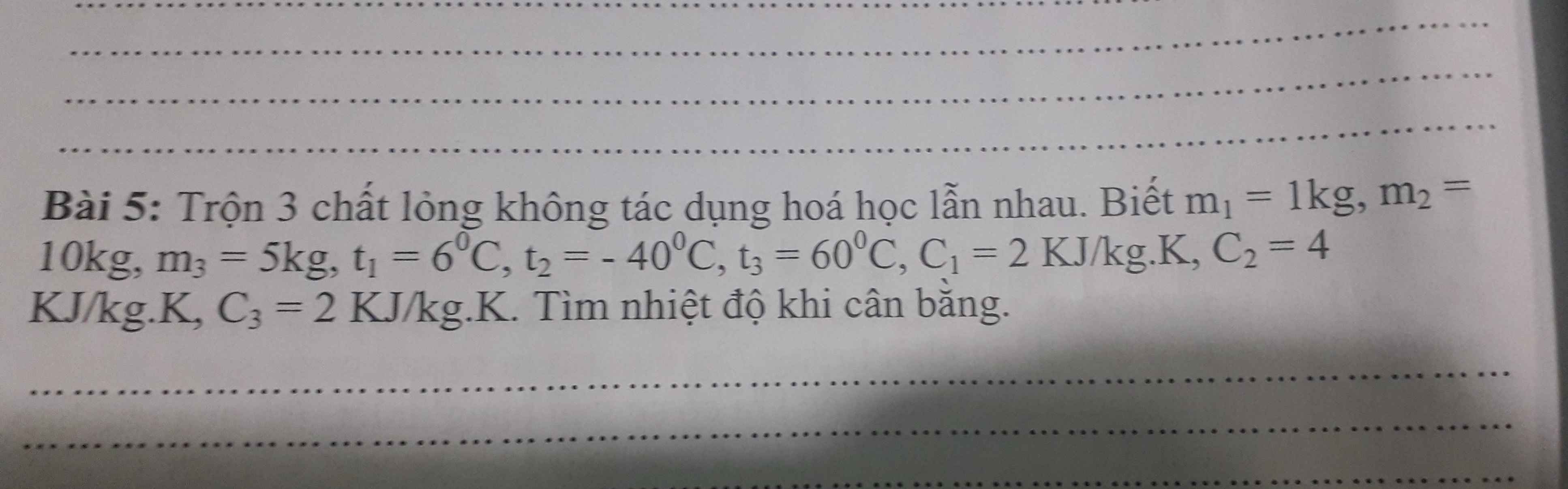
a) nhân dạng liên hiệp
<=> \(\dfrac{4\left(\sqrt{7}+3\right)}{2}-\dfrac{3\left(\sqrt{7}+2\right)}{3}\)
= 2\(\sqrt{7}+6-\sqrt{7}-2\) = \(\sqrt{7}+4\)
b) (\(\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}+1}-\sqrt{x}\)).\(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
<=> ( x - \(\sqrt{x}+1-\sqrt{x}\) ) . \(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
<=> \(\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}\)= \(\dfrac{\sqrt{x}-1}{\sqrt{x}}\)