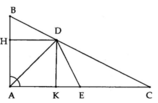
Cho tam giác ABC có  =120o . Tia phân giác của  cắt BC tại D. Tia phân giác của ADC ̂ cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đường thẳng AB, BC, AD. Chứng minh: a) AC là tia phân giác của DAH ̂ b) IH = IE = IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 10 2021
b: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
CM
31 tháng 7 2018
c) Do DH vuông góc với AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK. Suy ra điểm D cách đều AB và AC.
9 tháng 2 2023
a: Xét ΔIAB và ΔIDC có
IA=ID
AB=DC
IB=IC
=>ΔIAB=ΔIDC
=>góc IAB=góc IDC=góc IAD
=>AI là phân giác của góc BAC
b: Xét ΔAEI vuông tại E và ΔAHI vuông tại H có
AI chung
góc EAI=góc HAI
=>ΔAEI=ΔAHI
=>AE=AH; IE=IH
=>AI là trung trực của EH
D
23 tháng 1 2022
a) Xét ▲ABD và ▲ACD có:
\(\widehat{BAD}=\widehat{CAD}\) (AD là đường phân giác của \(\widehat{BAC}\))
AB=AC (▲ABC cân tại A).
AD là cạnh chung.
=>▲ABD = ▲ACD (c-g-c)
=> BD=CD (2 cạnh tương ứng) hay D là trung điểm BC. (1)
\(\widehat{ADB}=\widehat{ADC}\) (2 góc tương ứng)
Mà \(\widehat{ADB}+\widehat{ADC}=180^0\) (kề bù)
=>\(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD⊥BC tại D (2)
- Từ (1) và (2) suy ra: AD là đường trung trực của BC.
b) Xét ▲AIF và ▲AIE có:
\(\widehat{FAI}=\stackrel\frown{EAI}\) (AI là đường phân giác của \(\widehat{FAE}\) )
AF=AE (gt)
AI là cạnh chung.
=>▲AIF = ▲AIE (c-g-c)
=>\(\widehat{AFI}=\widehat{AEI}\) (2 góc tương ứng)
Mà\(\widehat{AEI}=90^0\)(BE⊥AC tại E)
=>\(\widehat{AFI}=90^0\) hay IF⊥AB tại F.
c) Xét ▲ABC có:
AD là đường cao (AD⊥BC tại I)
BE là đường cao (BE⊥AC tại E)
AD cắt BE tại I (gt)
=> I là trực tâm của ▲ABC.
=>CI⊥AB mà IF⊥AB (cmt)
=>CI trùng với IF hay C,I,F thẳng hàng.
28 tháng 3 2023
a: Xet ΔADB và ΔADE có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
b: Xét ΔAHD vuông tại HvàΔAKD vuông tại K co
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
=>DH=DK
=>D cách đều AB,AC
tham khảo
hình