Cho a/b=c/d. Chứng minh a/3a+b=c/3c+d (3 cách)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 5 2022
Đặt a/b=c/d=k
=>a=bk; c=dk
a: \(\dfrac{3a-c}{3b-d}=\dfrac{3bk-dk}{3b-d}=k\)
\(\dfrac{2a+3c}{2b+3d}=\dfrac{2bk+3dk}{2b+3d}=k\)
Do đó: \(\dfrac{3a-c}{3b-d}=\dfrac{2a+3c}{2b+3d}\)
c: \(\dfrac{a^2-b^2}{c^2-d^2}=\dfrac{b^2k^2-b^2}{d^2k^2-d^2}=\dfrac{b^2}{d^2}\)
\(\dfrac{2ab+b^2}{2cd+d^2}=\dfrac{2\cdot bk\cdot b+b^2}{2\cdot dk\cdot d+d^2}=\dfrac{b^2}{d^2}\)
Do đó: \(\dfrac{a^2-b^2}{c^2-d^2}=\dfrac{2ab+b^2}{2cd+d^2}\)
ND
0
5 tháng 10 2016
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(\Rightarrow\begin{cases}a=bk\\c=dk\end{cases}\)
Ta có :
\(\frac{a}{3a+b}=\frac{bk}{3bk+b}=\frac{bk}{b\left(3k+1\right)}=\frac{k}{3k+1}\left(1\right)\)
\(\frac{c}{3c+d}=\frac{dk}{3dk+d}=\frac{dk}{d\left(3k+1\right)}=\frac{k}{3k+1}\left(2\right)\)
Từ 1 và 2
=> \(\frac{a}{3a+b}=\frac{c}{3c+d}\)
5 tháng 10 2016
Giải:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(\Rightarrow a=b.k,c=d.k\)
Ta có:
\(\frac{a}{3a+b}=\frac{b.k}{3.b.k+b}=\frac{b.k}{b.\left(3.k+1\right)}=\frac{k}{3.k+1}\) (1)
\(\frac{c}{3c+d}=\frac{d.k}{3.d.k+d}=\frac{d.k}{d.\left(3.k+1\right)}=\frac{k}{3.k+1}\) (2)
Từ (1) và (2) suy ra \(\frac{a}{3a+b}=\frac{b}{3c+d}\)
25 tháng 11 2015
a/b=c/d => a/c=b/d
Mà a/c=3a/3c
=> 3a/3c=b/d
Áp dụng t/c của dãy tỉ số bằng nhau , ta có :
3a/3c=b/d = 3a+b/ 3c+d
Ta có a/c=3a+b/3c+d
=> a/3a+b=c/3c+4
19 tháng 8 2021
a, Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{3a}{3c}\)
Áp dụng tính chất của day tỉ số bằng nhau ta được:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{3a}{3c}=\dfrac{3a+b}{3c+d}\)
\(=>\dfrac{a}{c}=\dfrac{3a+b}{3c+d}=>\dfrac{a}{3a+b}=\dfrac{c}{3c+d}=>\left(đpcm\right)\)
S
19 tháng 8 2021
Bài 1:
Ta có:\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{3a}{3c}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{3a}{3c}=\dfrac{3a+b}{3c+d}\)
⇒\(\dfrac{a}{c}=\dfrac{3a+b}{3c+d}\Rightarrow\dfrac{a}{3a+b}=\dfrac{c}{3c+d}\)
Vậy từ tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{3a+b}=\dfrac{c}{3c+d}\)(ĐPCM)
DN
3
21 tháng 7 2016
\(\frac{a}{b}=\frac{c}{d}\)=> \(\frac{a}{c}=\frac{b}{d}\)
=> \(\frac{3a}{3c}=\frac{5b}{5d}\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\frac{3a}{3c}=\frac{5b}{5d}=\frac{3a-5b}{3c-5d}=\frac{3a+5b}{3c+5d}\)
=> Đpcm
Chúc bạn làm bài tốt
3 tháng 12 2017
vì a/b= c/d
⇒ a+b/c+d=3a+5b/3c+5d=3a-5b/3c-5d
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
3a+5b/3c+5d=3a-5b/3c-5d
⇒ 3a+5b/3a-5b=3c+5d/3c-5d (đpcm)
20 tháng 7 2015
Theo dãy tỉ số (=) ta* có:
\(\frac{a}{3b}=\frac{b}{3c}=\frac{c}{3d}=\frac{d}{3a}=\frac{a+b+c+d}{3a+3b+3c+3d}=\frac{a+b+c+d}{3\left(a+b+c+d\right)}=\frac{1}{3}\)
=> a = 1/3 . 3b = b (1)
=> b = 1/3 . 3c = c (2)
=> c = 1/3 . 3d = d (3)
Từ(1) (2) và (3) =. a = b= c =d => ĐPCM
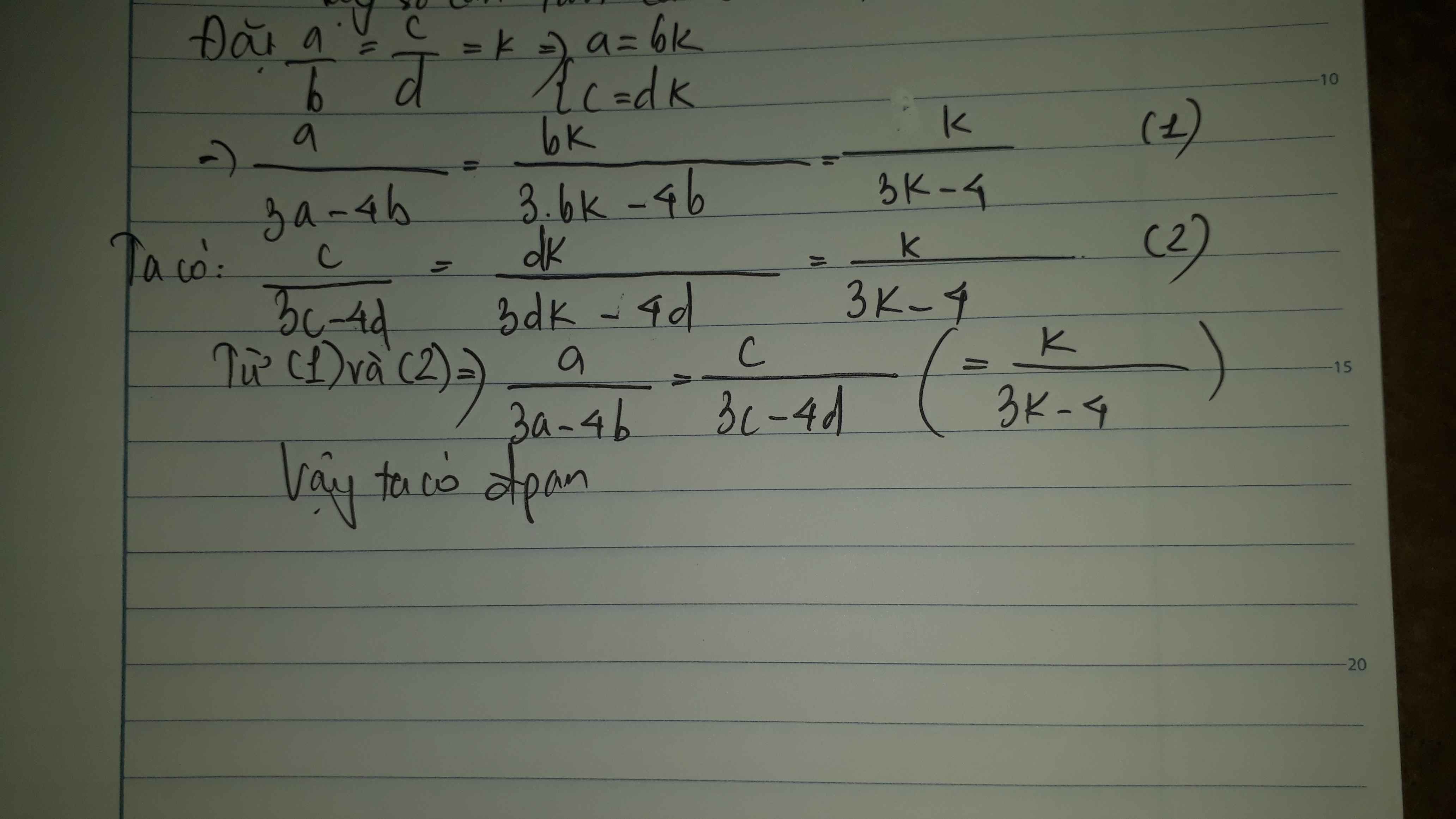
\(Cách\)\(1:\)
\(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\text{a=bk;c=dk (1)}\)
Ta có:\(\frac{a}{3a+b}=\frac{c}{3c+d}\)(thay(1) vào)
Ta dc:\(\frac{bk}{3bk+b}=\frac{bk}{b\left(3k+1\right)}=\frac{k}{3k+1}\left(2\right)\)(tiếp tục thay 1 vào)
\(\frac{dk}{3dk+1}=\frac{k}{3k+1}\)
\(Từ\)\(\left(1\right);\left(2\right)\RightarrowĐPCM\)
\(Cách\)\(2:\)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Rightarrow3ac+ad=3ac+bc\)
\(\Rightarrow\text{a(3c+d)=c(3a+b)}\Rightarrow\frac{a}{3a+b}=\frac{c}{3c+d}\left(ĐPCM\right)\)
Chúc bn hok tốt!!!