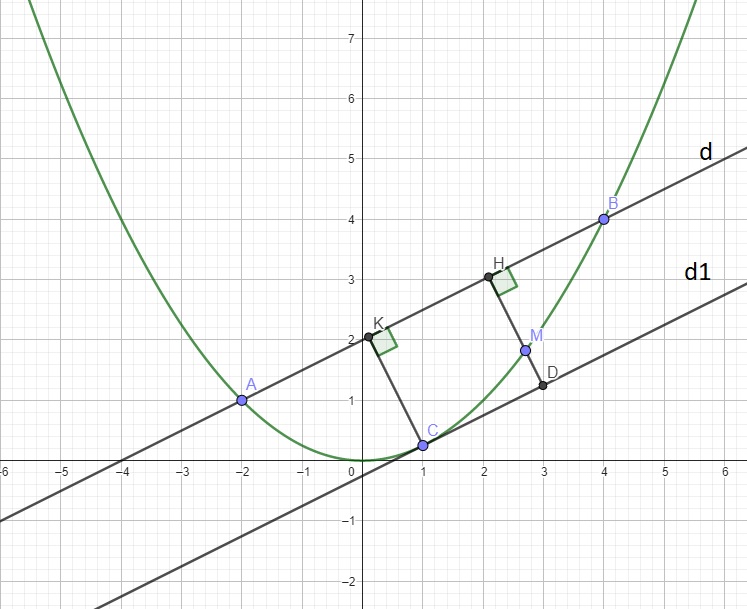
Cho parabol (P) \(y=\dfrac{1}{2}x^2\) và điểm A, B thuộc (P) có hoành độ lần lượt là: -1, 2. Đường thẳng (d) phương trình y=mx+n
a) Tìm tọa độ điểm A, B. Tìm m, n biết (d) đi qua A và B.
b) Tính độ dài đường cao OH của tam giác OAB (điểm O là gốc tọa độ)