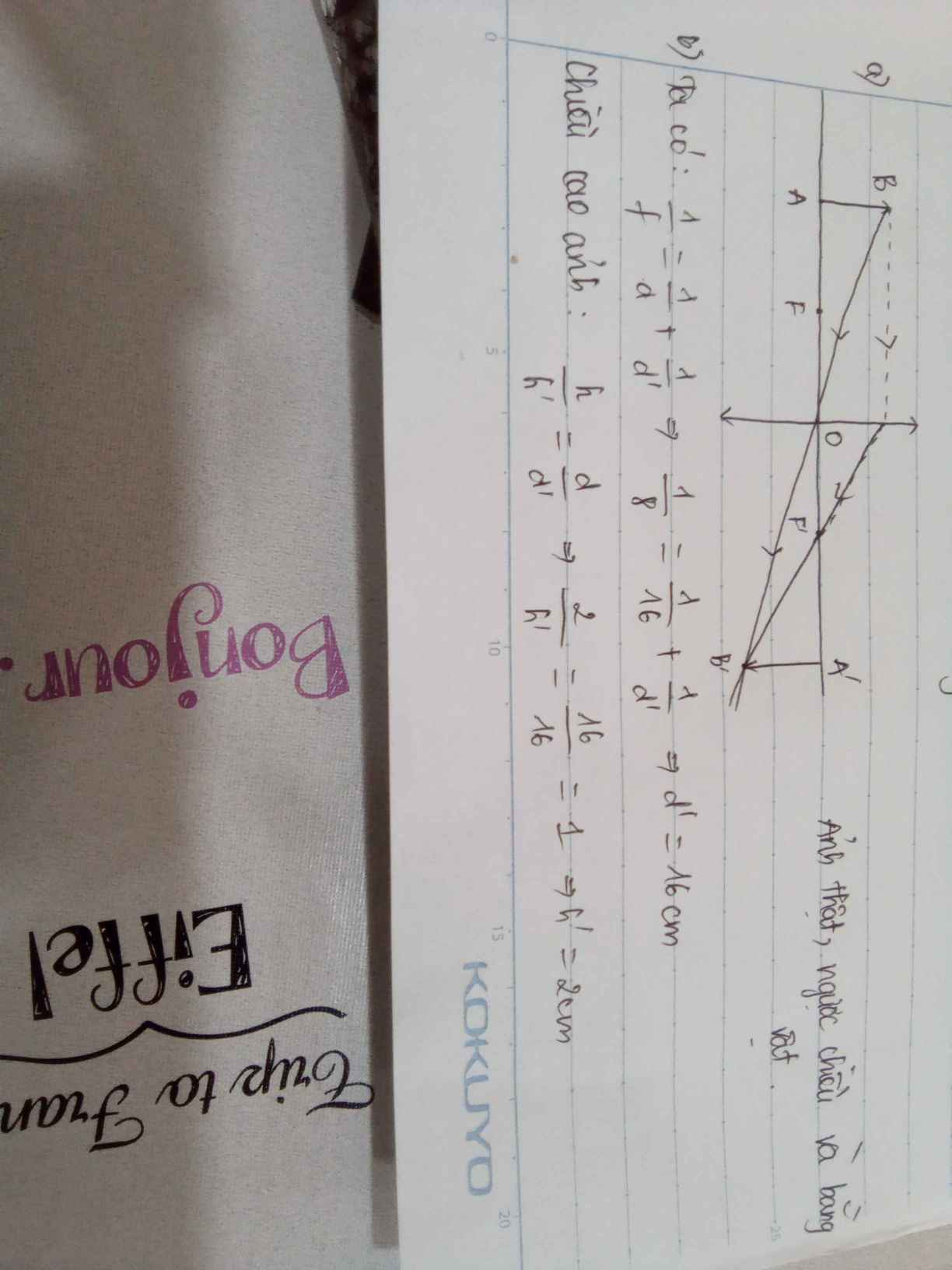
Một thấu kính hội tụ quang tâm O, tiêu cự f. Đặt một vật AB vuông góc với trục chính
của thấu kính (A ở trên trục chính) trước thấu kính một đoạn d, cho ảnh A'B' rõ nét hứng được
trên màn (màn vuông góc với trục chính) cách thấu kính một đoạn d'.
a) Chứng minh:
'
1/d=1/d+1/d'
= +
b) Biết thấu kính này có tiêu cự f = 12,5 cm và L là khoảng cách từ vật AB đến ảnh A'B'.
Hỏi L nhỏ nhất là bao nhiêu để có được ảnh rõ nét của vật ở trên màn?
c) Cho L = 90 cm. Xác định vị trí của thấu kính.
Mọi người giúp e gấp với ạ em xin cảm ơn!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Giữa độ bội giác và tiêu cự f (đo bằng cm) có hệ thức: 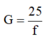

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=30cm\)

-Vẽ trục chính.
-Dựng quang tâm O.
-Dựng OF=5cm, OA=15cm.Lấy F' đối xứng với F qua O.
-Từ A vẽ ảnh AB thẳng đứng, vuông góc với trục chính.
-Nối B với O.
-Qua B kẻ đường thẳng song song với trục chính và đi qua F'.
-Hai đường thẳng trên cắt nhau tại đâu là điểm B'. Từ B' dựng vuông góc với trục chính đc ảnh A'B'.

a. Dựng ảnh A'B'

b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm