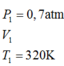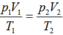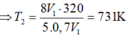Một binh kín chứa một lượng khí ở nhiệt độ 27 độ C và áp suất 1 atm. Hãy vẽ đồ thị biểu diễn sự biến thiên của áp suất theo nhiệt độ trong quá trình nung nóng đẳng tích lên tới nhiệt độ 127 độ C trong hệ tọa độ áp suất-nhiệt độ tuyệt đối (p, T)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3 2022
Trạng thái 1: \(\left\{{}\begin{matrix}p_1=2\cdot10^5Pa\\T_1=27^oC=300K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=???\\T_2=627^oC=900K\end{matrix}\right.\)
Quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{2\cdot10^5}{300}=\dfrac{p_2}{900}\)
\(\Rightarrow p_2=6\cdot10^5Pa\)
VT
8 tháng 11 2018
Do bình không dãn nở vì nhiệt, nên công do khí sinh ra : A' = p ∆ V = 0. Theo nguyên lí I, ta có :
∆ U = Q (1)
Nhiệt lượng do khí nhận được : Q = m c V ( T 2 - T 1 ) (2)
Mặt khác, do quá trình là đẳng tích nên :
Từ (2) tính được : Q = 15,58. 10 3 J.
Từ (1) suy ra: ∆ U = 15,58. 10 3 J.
VT
29 tháng 1 2017
- Chỉ ra đây là quá trình đẳng tích
- Áp dụng định luật Sác – lơ:
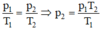
Thay số được p 2 = 4atm.
SS
26 tháng 4 2016
1/ Quá trình biến đổi trạng thái khi thể tích không đổi gọi là đẳng tích
Định luật: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối
Biểu thức:
\(\frac{P}{T}=\) hằng số
+Lưu ý: Nếu gọi \(P_1,T_1\) là áp suất và nhiệt độ tuyệt đối của 1 lượng khí ở trạng thái 1
Nếu gọi \(P_2,T_2\) là áp suất và nhiệt độ tuyệt đối của 1 lượng khí ở trạng thái 2
Ta có biểu thức: \(\frac{P_1}{T_1}=\frac{P_2}{T_2}\)
2/ Phương trình trạng thái khí lí tưởng:
\(\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}\)
Tính ra \(p_2=2,58atm\)
HQ
17 tháng 2 2021
Tóm tắt đề bài như sau:
\(\left\{{}\begin{matrix}V=10\left(l\right)\\p=2\left(atm\right)\\T=87+273=360\left(K\right)\end{matrix}\right.\underrightarrow{Đẳngáp}\left\{{}\begin{matrix}V_1=?\\p_1=2\left(atm\right)\\T_1=\dfrac{T}{2}=180\left(K\right)\end{matrix}\right.\) \(\underrightarrow{Đẳngnhiet}\left\{{}\begin{matrix}V_2=?\\p_2=0,5\left(atm\right)\\T_2=180\left(K\right)\end{matrix}\right.\)
Phương trình trạng thái khí lí tưởng ( Claperon Mendeleep ): \(\dfrac{pV}{T}=const\)
Đẳng áp: \(\dfrac{V}{T}=\dfrac{V_1}{T_1}\Leftrightarrow V_1=\dfrac{10.180}{360}=5\left(l\right)\)
Đẳng nhiệt: \(p_1V_1=p_2V_2\Rightarrow V_2=\dfrac{p_1V_1}{p_2}=\dfrac{2.5}{0,5}=20\left(l\right)\)
Vậy thể tích sau cùng của khối khí trên là V2=20(l)
2 tháng 12 2021
Ta có: \(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{5}{37+273}=\dfrac{p_2}{17+273}\)
\(\Rightarrow p_2=4,68atm\)
