Thầy Nguyễn Việt Lâm giúp em với ạ
K
Khách
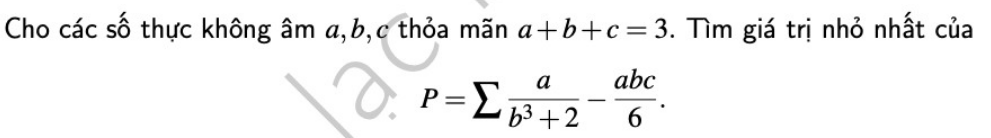
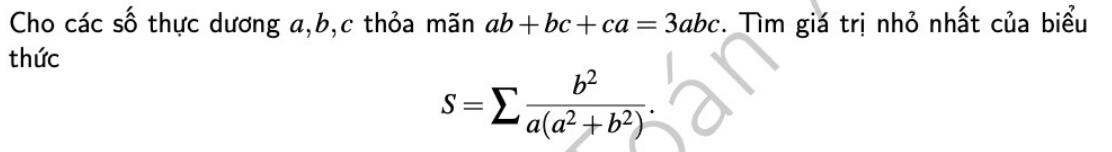
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
5.
\(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ac}+\sqrt{ab}\)
\(\Rightarrow\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự:
\(\dfrac{b}{b+\sqrt{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\dfrac{c}{c+\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng vế với vế:
\(P\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
6.
\(P=\dfrac{a}{1+b-a}+\dfrac{b}{1+c-b}+\dfrac{c}{1+a-c}\)
Thay \(1=a+b+c\)
\(\Rightarrow P=\dfrac{a}{2b+c}+\dfrac{b}{2c+a}+\dfrac{c}{2a+b}\)
\(P=\dfrac{a^2}{2ab+ac}+\dfrac{b^2}{2bc+ab}+\dfrac{c^2}{2ac+bc}\)
\(P\ge\dfrac{\left(a+b+c\right)^2}{3ab+3bc+3ca}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
L2
3
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2022
4.
\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)
\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2022
5.
Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
Đặt vế trái là P
\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)
Quay lại dòng 3 của bài số 4
H
2
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
1.
\(\left(x+y\right)^2=\left(\dfrac{1}{2}.2x+\dfrac{1}{3}.3y\right)^2\le\left(\dfrac{1}{4}+\dfrac{1}{9}\right)\left(4x^2+9y^2\right)=\dfrac{169}{36}\)
\(\Rightarrow-\dfrac{13}{6}\le x+y\le\dfrac{13}{6}\)
Dấu "=" lần lượt xảy ra tại \(\left(-\dfrac{3}{2};-\dfrac{2}{3}\right)\) và \(\left(\dfrac{3}{2};\dfrac{2}{3}\right)\)
2.
\(\left(y-2x\right)^2=\left(\dfrac{1}{4}.4y+\left(-\dfrac{1}{3}\right).6x\right)^2\le\left(\dfrac{1}{16}+\dfrac{1}{9}\right)\left(16y^2+36x^2\right)=\dfrac{25}{16}\)
\(\Rightarrow\left|y-2x\right|\le\dfrac{5}{4}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\mp\dfrac{2}{5};\pm\dfrac{9}{20}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
3.
\(B^2=\left(6.\sqrt{x-1}+8\sqrt{3-x}\right)^2\le\left(6^2+8^2\right)\left(x-1+3-x\right)=200\)
\(\Rightarrow B\le2\sqrt{10}\)
Dấu "=" xảy ra khi \(\dfrac{\sqrt{x-1}}{6}=\dfrac{\sqrt{3-x}}{8}\Leftrightarrow x=\dfrac{43}{25}\)
\(B=6\sqrt{x-1}+6\sqrt{3-x}+2\sqrt{3-x}\ge6\sqrt{x-1}+6\sqrt{3-x}\)
\(B\ge6\left(\sqrt{x-1}+\sqrt{3-x}\right)\ge6\sqrt{x-1+3-x}=6\sqrt{2}\)
\(B_{min}=6\sqrt{2}\) khi \(\sqrt{3-x}=0\Rightarrow x=3\)
4.
\(49=\left(3a+4b\right)^2=\left(\sqrt{3}.\sqrt{3}a+2.2b\right)^2\le\left(3+4\right)\left(3a^2+4b^2\right)\)
\(\Rightarrow3a^2+4b^2\ge\dfrac{49}{7}=7\)
Dấu "=" xảy ra khi \(a=b=1\)
TB
2
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2021
(O) và (D) cắt nhau tại A và M \(\Rightarrow AM\perp OD\)
\(\Rightarrow\widehat{AOD}=\widehat{ABN}\) (cùng phụ \(\widehat{BAM}\))
\(\Rightarrow OD||BN\) (góc đồng vị bằng nhau)
\(\Rightarrow OBND\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow OB=DN\), mà \(\left\{{}\begin{matrix}AB=DC\\OB=\dfrac{1}{2}AB\end{matrix}\right.\) \(\Rightarrow OB=\dfrac{1}{2}CD\Rightarrow DN=\dfrac{1}{2}DC\Rightarrow N\) là trung điểm CD
Like cho mình nhé !!
AH
Akai Haruma
Giáo viên
24 tháng 3 2023
Lời giải:
Áp dụng BĐT AM-GM:
$\frac{x^2}{y+z}+\frac{y+z}{4}\geq 2\sqrt{\frac{x^2}{y+z}.\frac{y+z}{4}}=x$
$\frac{y^2}{x+z}+\frac{x+z}{4}\geq y$
$\frac{z^2}{x+y}+\frac{x+y}{4}\geq z$
Cộng theo vế các BĐT trên và thu gọn ta được:
$P\geq \frac{x+y+z}{2}=\frac{2}{2}=1$
Vậy $P_{\min}=1$ khi $x=y=z=\frac{2}{3}$
DN
0
7 tháng 3 2016
Uừm chắc tại cậu hay hỏi nhưng câu hoi như là: 1+1 hay là cậu trả lời linh tinh như là thiếu dề rôi chẳng hạn...bị 1 lần thì chắc ko sao nhưng nếu mà lặp lại nhiều lần thì online math sẽ xóa tài khoản luôn đấy!
Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ - Hoc24