Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, \(\widehat{BAD}=120^o\). Biết \(SA\perp BD,SB\perp AD\) và (SBD) tạo với mặt phẳng (ABCD) góc \(60^o\). Lấy H đối xứng với C qua A.
a) Tính \(V_{S.ABCD}\)
b) Gọi các điểm M, N lần lượt thuộc các cạnh SC, SD sao cho \(SM=\dfrac{a\sqrt{43}}{4};SN=\dfrac{a\sqrt{39}}{6}\). Tính \(V_{AMND}\).

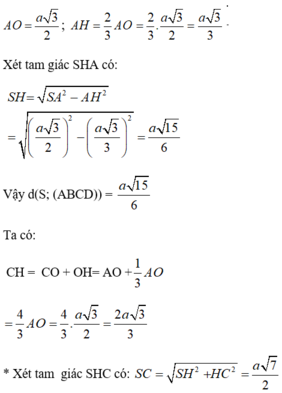





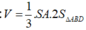
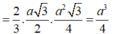
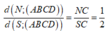
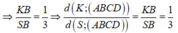
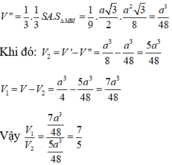
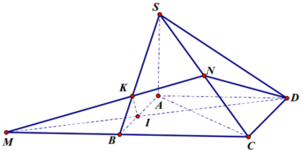
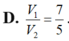
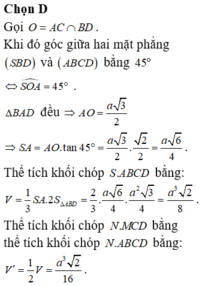
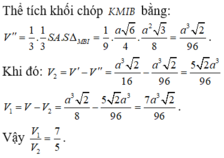

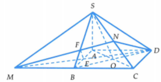
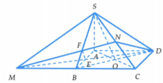
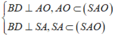
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}=60^0\Rightarrow\) các tam giác ABC và ACD là các tam giác đều
\(AH=AC\Rightarrow AH=AC=AB\Rightarrow\Delta HBC\) vuông tại B
\(\Rightarrow HB\perp BC\Rightarrow HB\perp AD\)
Qua H kẻ đường thẳng \(d\perp\left(ABCD\right)\Rightarrow S\in d\)
Gọi O là giao điểm AC và BD, do góc giữa (SBD) và đáy bằng 60 độ
\(\Rightarrow\widehat{SOH}=60^0\)
\(\Rightarrow SH=OH.tan60^0=\left(AH+AO\right).tan60=\left(a+\dfrac{a}{2}\right).tan60^0=\dfrac{3a\sqrt{3}}{2}\)
\(V_{S.ABCD}=\dfrac{1}{3}SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{3a\sqrt{3}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3}{4}\)
b.
\(SC=\sqrt{SH^2+HC^2}=\sqrt{SH^2+\left(2AC\right)^2}=\dfrac{a\sqrt{43}}{2}\)
\(\Rightarrow M\) là trung điểm SC \(\Rightarrow AM\) là đường trung bình tam giác SHC
\(\Rightarrow\left\{{}\begin{matrix}AM||SH\Rightarrow AM\perp\left(ABCD\right)\\AM=\dfrac{1}{2}SH=\dfrac{3a\sqrt{3}}{4}\end{matrix}\right.\)
\(HD=\sqrt{OD^2+OD^2}=\sqrt{\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2}=a\sqrt{3}\)
\(\Rightarrow SD=\sqrt{SH^2+HD^2}=\dfrac{a\sqrt{39}}{2}\Rightarrow SN=\dfrac{1}{3}SD\Rightarrow ND=\dfrac{2}{3}SD\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}d\left(S;\left(MAD\right)\right)\)
Mà \(SH||\left(MAD\right)\Rightarrow d\left(S;\left(MAD\right)\right)=d\left(H;\left(MAD\right)\right)\)
Gọi E là giao điểm BH và AD, ta có:
\(\left\{{}\begin{matrix}HB\perp AD\left(cmt\right)\\AM\perp\left(ABCD\right)\Rightarrow AM\perp HB\end{matrix}\right.\) \(\Rightarrow HB\perp\left(MAD\right)\)
\(\Rightarrow HE=d\left(H;\left(MAD\right)\right)\)
\(HE=\dfrac{1}{2}HB=\dfrac{1}{2}HD=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left(N;\left(MAD\right)\right)=\dfrac{2}{3}HE=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{AMND}=\dfrac{1}{3}.d\left(N;\left(MAD\right)\right).\dfrac{1}{2}AM.AD=\dfrac{a^3}{8}\)