Viết phương trình tham số của đường thẳng d đi qua điểm M(-3;5) và song song với đường phân giác của góc phần tư thứ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do d \(\left\{{}\begin{matrix}điquaM\left(2;6\right)\\vtcp\overrightarrow{u}=\left(2;-3\right)\end{matrix}\right.\)
=> Pt tham số: \(\left\{{}\begin{matrix}x=2+2t\\y=6-3t\end{matrix}\right.\)

Đáp án D
Mặt phẳng (P) có vecto pháp tuyến là: n p → (3; 1; 0)
Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: u d → = n p → (3; 1; 0)
Phương trình tham số của đường thẳng d:
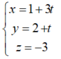
Chọn D.

a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0

Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
Tại sao từ cos 450=\(\dfrac{\sqrt{2}}{2}\) thì lại => a=3b hoặc a=\(\dfrac{-b}{3}\) ạ ?

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

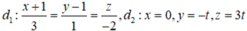

Đường phân giác của góc phần tư thứ nhất có 1 vtcp là (1;1)
\(\Rightarrow\) d cũng nhận (1;1) là 1 vtcp
Phương trình: \(\left\{{}\begin{matrix}x=-3+t\\y=5+t\end{matrix}\right.\)