CMR: trong tam giác vuông đường cao tương ứng với cạnh huyền không lớn hơn nửa cạnh huyền.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác vuông ABC, vuông tại A, có AM là trung tuyến.
Trên tia đối của tia MA lấy điểm D sao cho DM = AM.
=> AM = \(\dfrac{1}{2}\) AD (1)
=> Tứ giác ABCD là hình bình hành, có góc A = \(90^0\) nên ABDC là hình chữ nhật.
=> AD = BC (2)
Từ (1) và (2) => AM = \(\dfrac{1}{2}\) BC (đpcm).
Vậy trong một tam giác vuông, trung tuyến tương ứng với cạnh huyền bằng nửa cạnh huyền.

Giả sử tam giác ABC có góc (BAC) = 90 ° , AH ⊥ BC, BC = 5, AH = 2 và BH < CH
Ta có: BH + CH = 5 (1)
Theo hệ thức liên hệ giữa đường cao và cạnh huyền trong tam giác, ta có:
BH.CH = A H 2 = 2 2 = 4 (2)
Từ (1) và (2) suy ra: BH = 1 và CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A B 2 = BH.BC = 1.5 = 5
Suy ra: AB = 5

k mk nha
đúng
Bài giải:
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.

Cách khác (theo cách lớp 7):
Xét tam giác ABC vuông tại A,trung tuyến AD.Ta cần chứng minh: \(AD=\frac{1}{2}BC\)
Ta chứng minh ngược lại,tức là \(AD\ne\frac{1}{2}BC\)
+ Nếu \(AD>\frac{1}{2}BC\Rightarrow\widehat{B}>\widehat{A_2},AD>CD\Leftrightarrow\widehat{C}>\widehat{A}\) (Đ.lí về cạnh đối diện với góc trong tam giác)
Hay \(\widehat{B}+\widehat{C}>\widehat{A_2}+\widehat{A_1}=90^o>\widehat{A}\) (mâu thuẫn với giả thiết)
+ Chứng minh tương tự với \(AD< \frac{1}{2}BC\) được: \(\widehat{B}+\widehat{C}< \widehat{A_2}+\widehat{A_1}\Leftrightarrow90^o< \widehat{A}\) (mâu thuẫn)
Vậy ta luôn có: \(AD=\frac{1}{2}BC\) (đpcm)
Tam giác vuông ABC, vuông tại A, có AM là trung tuyến
trên tia đối của MA lấy điểm D sao cho MD=AM
Do đó AM=1/2 AD (1)
suy ra tứ giác ABDC là hình bình hành, có ^A=90*
nên ABDC là hình chữ nhật
suy ra AD=BC (2)
Từ (1) và (2) ta có AM = 1/2 BC
Vậy trong 1 tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

Gọi độ dài cạnh góc vuông 1 là x
=>Độ dài cạnh góc vuông 2 là x+2
Theo đề, ta có: x^2+x^2+4x+4=5^2=25
=>2x^2+4x-21=0
=>x=(-2+căn 46)/2
=>Độ dài cạnh góc vuông 2 là (2+căn 46)/2
Độ dài đường cao là:
\(\dfrac{\left(-2+\sqrt{46}\right)\left(2+\sqrt{46}\right)}{2}:5=\dfrac{46-4}{2}:5=\dfrac{42}{10}=4,2\)

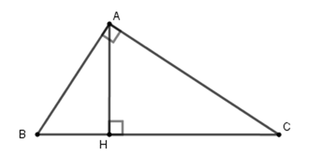
Giả sử tam giác đã cho là ABC vuông tại A có AB < AC, BC = 5; AH = 2
Đặt BH = x (0 < x < 2,5) => HC = 5 – x
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
![]()
=> (x – 1)(x – 4) = 0
⇔ x − 1 = 0 x − 4 = 0 ⇔ x = 1 t m x = 4 k t m
![]()
Vậy cạnh nhỏ nhất của tam giác đã cho có độ dài là 5
Đáp án cần chọn là: A
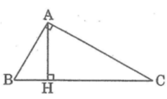
xét tam giác ABC vuông tại cao có đường cao AH và đường trung tuyến AM
khi đó tam giác AHM là tam giác vuông tại H nên
ta có \(AH\le AM\text{ mà }AM=\frac{1}{2}BC\)
nên ta có
Mình có 2 cách bạn chọn cách nào cũng được nhé.
Cách 1: Giả sử tam giác ABC vuông tại A có đường cao AH . Khi đó, theo hệ thức lượng trong tam giác vuông, ta có:
\(AH^2=BH.CH\)\(\Rightarrow AH=\sqrt{BH.CH}\)
Mặt khác nửa cạnh huyền chính là \(\frac{BC}{2}=\frac{BH+CH}{2}\)
Theo BĐT Cô-si, ta có \(\sqrt{BH.CH}\le\frac{BH+CH}{2}\)hay \(AH\le\frac{BC}{2}\)
Dấu "=" xảy ra khi \(BH=CH\)\(\Rightarrow\)đường cao AH cũng là trung tuyến \(\Rightarrow\Delta ABC\)vuông cân tại A.
Cách 2: Giả sử tam giác ABC vuông tại A có đường cao AH, trung tuyến AM.
Ta ngay lập tức có được \(AM=\frac{BC}{2}\)
Vì AH, AM lần lượt là đường vuông góc và đường xiên hạ từ A đến BC \(\Rightarrow AH\le AM\)hay \(AH\le\frac{BC}{2}\)
Dấu "=" xảy ra khi \(AH\equiv AM\)hay \(\Delta ABC\)vuông cân tại A.