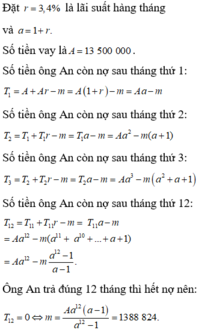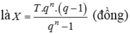Mẹ An mua một chiếc ti vi giá 15 790 000 nghìn đồng theo hình thức thanh
toán như sau: trả trước 40% và kết hợp trả góp mỗi tháng 500 000 nghìn đồng. Tính
tổng số tiền mẹ An phải trả?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
26 tháng 3 2015
Cô bán hàng trả : 50 000 - (15 000 + 25 000) = 10 000 ( đồng )
DH
26 tháng 3 2015
Cô bán hàng phải trả:50000-(15000+25000)=1000(đồng)
Đáp số:1000 đồng
9 tháng 10 2022
Đáp án:
Giải thích các bước giải:
Để bác bán hàng không phải trả tiền thừa, Tuấn
cần trả:
+ Mệnh giá đồng: tờ
+ Mệnh giá đồng: tờ
+ Mệnh giá đồng: tờ
Làm như trên vì × + × + × =
24 tháng 12 2016
Gọi số tiền còn lại phải trả sau i tháng là Pi ; A=300 (triệu) là số tiền đã vay ; d=5,5 (triệu) là số tiền trả cố định tháng ; r=0,5% là lãi trên tháng
Ta luôn có, tại thời điểm tháng thứ i, số tiền còn lại phải trả là Pi bằng số tiền còn lại phải trả của tháng trước đó trừ đi tiền lãi ( Pi-1*r ) và trừ thêm tiền trả cố định hàng tháng (d) ; viết gọn lại là \(P_i=P_{i-1}-P_{i-1}\cdot r-d=P_{i-1}\left(1-r\right)-d\)
Áp dụng côn thức trên ta có:
Ngay tại thời điểm vay xong thì \(P_0=A\)
qua tháng thứ nhất : \(P_1=P_0-P_0r-d=A\left(1-r\right)-d\)
qua tháng thứ hai : \(P_2=P_1\left(1-r\right)-d=A\left(1-r\right)^2-d\cdot\left[\left(1-r\right)+1\right]\)
.....
qua tháng thứ k : \(P_k=P_{k-1}\left(1-r\right)-d=A\left(1-r\right)^k-d\cdot\left[\left(1-r\right)^{k-1}+\left(1-r\right)^{k-2}+...+\left(1-r\right)+1\right]\\ =A\left(1-r\right)^k-d\cdot\frac{\left(1-r\right)^k-1}{\left(1-r\right)-1}\)
Xét thời điểm trả hết nợ, tức là Pk=0
\(\Leftrightarrow A\left(1-r\right)^k-d\cdot\frac{\left(1-r\right)^k-1}{\left(1-r\right)-1}=0\\ \Leftrightarrow300\left(1-0,5\%\right)^k=5,5\cdot\frac{\left(1-0,5\%\right)^k-1}{\left(1-0,5\%\right)-1}\\ \Leftrightarrow\left(1-0,5\%\right)^k=\frac{11}{14}\Leftrightarrow k\approx48,1117\)
Bạn nhớ luôn công thức tren để giải bài tập liên quan nhé
14 tháng 4 2023
Số tiền phải trả theo cách 2 là:
3290000*36%+360000*6=3344400(đồng)
=>Cách 2 phải trả nhiều hơn
