Cho tam giác ABC. Vẽ điểm D sao cho BAD và ABC là hai góc so le trong, BAD=ABC. Vẽ điểm E sao cho EAC và ACB là hai góc so le trong, EAC=ACB. Chứng tỏ rằng ba điểm D, A, E thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có B A M ^ = B ^ suy ra AM // BC (vì có cặp góc so le trong bằng nhau).
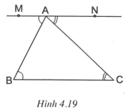
C A N ^ = C ^ suy ra AN // BC (vì có cặp góc so le trong bằng nhau).
Theo tiên đề Ơ-clít qua điểm A chỉ có một đường thẳng song song với BC, do đó ba điểm M, A, N thẳng hàng

a) Tia Am nằm giữa hai tia AC,AD vì C A D ^ = 80 ° > C A E ^ = 50 °
b) Điểm E nằm giữa hai điểm C, D vì tia Am nằm giữa hai tia AC, AD và ba điểm cùng nằm trên cạnh BC.
c) D A E ^ = 30°
d) B A D ^ = D A E ^ < E A C ^
e) A E B ^

b) Xét ΔCBD có CF là đường phân giác ứng với cạnh BD(gt)
nên \(\dfrac{FD}{FB}=\dfrac{CD}{CB}\)(Tính chất tia phân giác của tam giác)(1)
Xét ΔCBA có CE là đường phân giác ứng với cạnh BA(gt)
nên \(\dfrac{EB}{EA}=\dfrac{CB}{CA}\)(Tính chất tia phân giác của tam giác)(2)
Ta có: ΔABC\(\sim\)ΔBDC(cmt)
nên \(\dfrac{CB}{CD}=\dfrac{CA}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{CD}{CB}=\dfrac{CB}{CA}\)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{FD}{FB}=\dfrac{EB}{EA}\)(Đpcm)
a) Xét ΔABC và ΔBDC có
\(\widehat{BCD}\) chung
\(\widehat{BAC}=\widehat{DBC}\)(gt)
Do đó: ΔABC∼ΔBDC(g-g)

a: Xét ΔABC và ΔBDC có
góc C chung
góc BAC=góc DBC
=>ΔABC đồng dạng với ΔBDC
b: FD/FB=CD/CB
EB/EA=CB/CA
mà CD/CB=CB/CA
nên FD/FB=EB/EA