CÂU 1:cho hai tam giác đồng dạng có tỉ số chu vi là 7/3 và hiệu độ dài hai cạnh là 10 cm .Tính độ dài hai cạnh đó
giúp mình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 3 2018
Gọi độ dài cua tam giac lớn là A, B, C
GỌI................................nhỏ a, b ,c
suy ra: chu vi tam giac lớn là A+B+C=17
.................................nhỏ là a+b+c=15
ta co tỉ số đồng dạng sau:
a/A=b/B=c/C=(a+b+c)/(A+B+C)=15/17
sủy ra: a/A=15/17 (*)
mat khác:A-a =12,5 (do hieu 2 cạnh tương ứng =12,5) SUY RA: A=12,5+a thay vào (*)
ta được:a/(12,5+a)=15/17suy ra a=93,75 suy ra A=12,5+93,75=106,25
Xem thêm tại :các bạn gải hộ mình bài toán này nhé. mai mình phải nộp rồi? | Yahoo Hỏi & Đáp
15 tháng 5 2016
Gọi a là số bé, b là số lớn, ta có:a/b = 15/17 và b-a=12,5(*)
Ta có:a/b =15/17 => a=(15.b)/17, thay vào (*), ta được: b-(15.b)/17=12,5 => b=106,25; a=93,75
CM
20 tháng 2 2017
Giả sử ΔA’B’C’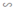 
ΔABC có hai cạnh tương ứng là A’B’ và AB có hiệu AB - A'B' = 12,5 (cm)
ΔA’B’C’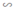 
ΔABC ⇒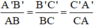 
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
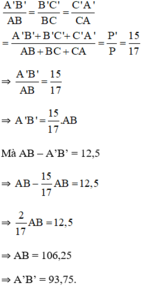
Vậy hai cạnh cần tìm là 106,25 và 93,75.
HB
22 tháng 4 2017
Giả sử có ΔABC ∼ ΔA'B'C' có hai cạnh tương ứng là AB và A'B' và có hiệu AB - A'B' = 12,5 (cm)
Do ΔABC ∼ ΔA'B'C' nên ta có
26 tháng 2 2018
Giả sử , ta có : ABC ~ A'B'C' ( \(A'B'-AB=12,5\left(cm\right)\) )
=> \(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}=\dfrac{AB+AC+BC}{A'B'+A'C'+B'C'}=\dfrac{15}{17}\)
=> \(\dfrac{AB}{15}=\dfrac{A'B'}{17}=\dfrac{A'B'-AB}{17-15}=\dfrac{12,5}{2}\)
=> \(\dfrac{A'B'}{15}=\dfrac{12,5}{2}\Rightarrow A'B'=106,25\left(cm\right)\)
\(\Rightarrow\dfrac{AB}{17}=\dfrac{12,5}{2}\Rightarrow AB=93,75\left(cm\right)\)
Vậy....
4 tháng 3 2018
Nếu ΔABC đồng dạng ΔA'B'C' có hai cạnh tương ứng là AB và A'B' có hiệu AB - A'B' = 12,5 (cm)
Vì ΔABC đồng dạng ΔA'B'C' nên
\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=\frac{A'B'+B'C'+A'C'}{AB+BC+AC}=\frac{C_{A'B'C'}}{C_{ABC}}=\frac{15}{17}\)
\(\Rightarrow\frac{A'B'}{AB-A'B'}=\frac{15}{17-15}=\frac{15}{2}\)
\(\frac{\Rightarrow A'B'}{12,5}=\frac{15}{2}\Rightarrow A'B'=\frac{15}{2}.12,5=93,75\left(cm\right)\)
\(AB-A'B'=12,5\Rightarrow AB=12,5+A'B'=12,5+93,75=106,25\left(cm\right)\)
Vậy A'B' = 93,75 và AB = 106,25 ( cm )
5 tháng 4 2022
Độ dài cạnh thứ nhất là:
48:4x1=12(cm)
Độ dài cạnh thứ hai là:
48-12=36(cm)
5 tháng 4 2022
Cạnh thứ nhất :
48 : 4 x 1 = 12 (cm)
Cạnh thứ hai :
48 - 12 = 36 (cm)
16 tháng 3 2022
Độ dài cạnh thứ nhất là:
63x3/7=27(m)
Độ dài cạnh thứ hai là 63-27=36(m)
Giả sử ta có: \(ΔABC\backsim ΔA'B'C'\\\to \dfrac{P_{ΔABC}}{P_{ΔA'B'C'}=\dfrac{7}{3}\\\to dfrac{AB}{A'B'}=\dfrac{7}{3}\end{cases}\)
\(\to \dfrac{AB}{7}=\dfrac{A'B'}{3}=\dfrac{AB-A'B'}{7-3}=\dfrac{10}{4}=\dfrac{5}{2}\\\to\begin{cases}AB=\dfrac{35}{2}\\A'B'=\dfrac{15}{2}\end{cases}\)
Vậy độ dài 2 cạnh lần lượt là \(\dfrac{35}{2};\dfrac{15}{2}\)