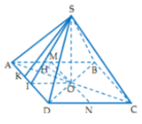
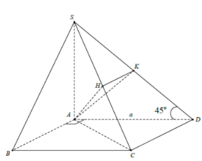
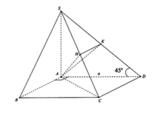
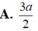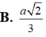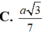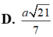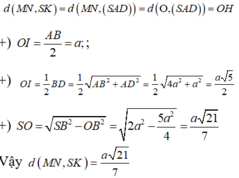Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài các cạnh bên của hình chóp bằng nhau và bằng 2 lần độ dài cạnh hình vuông.Gọi M và N lần lượt là trung điểm của AD và SD.Tính số đo của góc (MN,SC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 11 2017
Đáp án C
MN là đường trung bình của tam giác DAS nên MN//SA.
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên
CM
10 tháng 8 2017
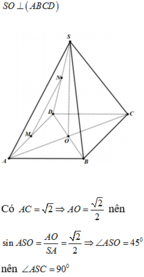
Đáp án C
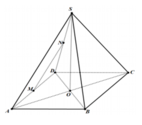
MN là đường trung bình của tam giác DAS nên MN//SA
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên SO ⊥ (ABCD)
CM
29 tháng 5 2017
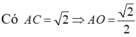
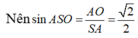
Đáp án D
Phương pháp:
- Tìm một mặt phẳng chứa SK mà song song với MN, đó chính là mặt phẳng (SAD)
- Từ đó ta chỉ cần tính khoảng cách từ MN đến (SAD).
Cách giải: Gọi I là trung điểm AD, AC cắt BD tại O. H là hình chiếu vuông góc của O trên SI.
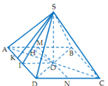
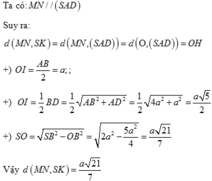
Chú ý khi giải: HS thường không chú ý đến phương pháp tìm mặt phẳng song song mà chỉ tập trung đi tìm đường vuông góc chung dẫn đến sự phức tạp cho bài toán và không đi đến được đáp án.
CM
26 tháng 10 2017
Chọn đáp án C.
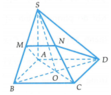
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O
CM
26 tháng 12 2018
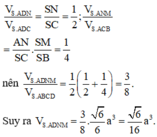
Đáp án A
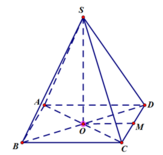
Gọi O là tâm của hình vuông, ta có
M S → . C B → = M S → .2 M O → = 2. ( M O → + O C → ) . M O → = 2 M O 2 + 0 = a 2 2
