Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE//IK, DE=IK.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 2 2018
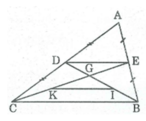
* Trong ∆ ABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ∆ ABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong ∆ GBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của ∆ GBC
⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.
OF
7 tháng 10 2020
* Trong ΔABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ΔABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong ΔGBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của ΔGBC⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.
5 tháng 8 2021
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(1)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình của ΔGBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra DE//IK và DE=IK
20 tháng 8 2016
Xét \(\Delta ABC\) có :
\(AE=EB\left(gt\right)\)
\(AD=DC\left(gt\right)\)
\(\Rightarrow ED\) là đường trung bình
\(\Rightarrow ED\)//\(BC\) và \(ED=\frac{1}{2}BC\) ( 1 )
Xét \(\Delta GBC\) có :
\(GI=IB\left(gt\right)\)
\(GK=KC\left(gt\right)\)
\(\Rightarrow IG\) là đường trung bình
\(\Rightarrow IG\)//\(BC\) và \(IG=\frac{1}{2}BC\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow DE\)//\(IK\) và \(DE\)=\(IK\)
20 tháng 8 2016
+) Tam giác ABC có D; E là trung điểm của AB; AC
=> DE là đường tring bình của tam giác => DE// BC và DE = BC/2 (1)
+) Tam giác GBC có I: K là Trung điểm của GB; GC
=> IK là đường trung bình của tam giác
=> IK //BC và IK = BC/ 2 (2)
Từ (1)(2) => DE//IK và DE = IK
D
18 tháng 7 2021
△ABC có:
- D là trung điểm của AC (gt)
- E là trung điểm của AB (gt)
=> DE là đường trung bình của △ABC
=> DE // BC
△GBC có:
- I là trung điểm của GB (gt)
- K là trung điểm của GC (gt)
=> IK là đường trung bình của △GBC
=> IK // BC
Mà DE // BC, IK // BC => DE // IK (đpcm)
Do DE là đường trung bình của △ABC => DE = 1/2 BC
IK là đường trung bình của △GBC => IK = 1/2 BC
Từ đó suy ra: DE = IK (đpcm)
18 tháng 7 2021
Xét ΔABC có
E là trung điểm của AB(gt)
D là trung điểm của AC(gt)
Do đó: DE là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
I là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: IK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra DE//IK và DE=IK(Đpcm)
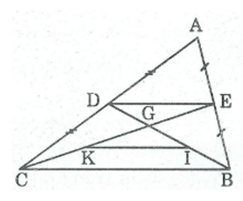
Cho tam giác ABC các đường trung tuyến BD và CE cắt nhau tại G gọi I và K theo thứ tự là trung điểm của GB GC
a tứ giác BIKC lF hình gì ? Vì sao?
b tú giác EDKI là hình gì ? Vì sao?