Một người kéo thùng hàng nặng 89kg lên cao 5m trong thời gian 15s, bỏ qua ma sát. Tính công, công suất của người đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
Công gây ra
\(A=P.h=150.5=750\left(J\right)\)
Công suất sinh ra là
\(P=\dfrac{A}{t}=\dfrac{750}{20}=37,5W\)
31 tháng 3 2023
Chọn hệ trục tọa độ Oxy như hình vẽ. Gọi \(\overrightarrow{F_k}\) là lực kéo tác dụng lên sợi dây, \(\overrightarrow{P}\) và \(\overrightarrow{N}\) lần lượt là trọng lực tác dụng lên vật. Ta phân tích \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}}\) và \(\overrightarrow{F_{k_y}}\) trên các trục Ox, Oy.
a) Công của lực kéo là \(A_k=F_k.s.cos\left(\overrightarrow{F_k},\overrightarrow{s}\right)=100.20.cos45^o=1000\sqrt{2}\left(J\right)\)
b) Gọi \(\overrightarrow{F_{ms}}\) là lực ma sát tác dụng lên vật. Chọn chiều dương là chiều chuyển động của vật
Áp dụng định luật II Newton:
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\) (1)
Chiếu (1) lên Oy: \(N=P-F_{k_y}=400-F_k.sin45^o=400-175\sqrt{2}\left(N\right)\)
Do đề bài không nói gì về loại chuyển động của vật nên mình sẽ xem đây là chuyển động nhanh dần đều nhé. Khi đó, ta sẽ có \(s=\dfrac{1}{2}at^2\Rightarrow20=\dfrac{1}{2}a.180^2\) \(\Rightarrow a=\dfrac{1}{810}\left(m/s^2\right)\).
Chiếu (1) lên Ox, ta được \(F_{k_x}-F_{ms}=m.a\Rightarrow F_{ms}=F_{k_x}-m.a=350.cos45^o-400.\dfrac{1}{180}\)\(=170\sqrt{2}-\dfrac{20}{9}\) (N)
\(\Rightarrow A_{ms}=-\left(170\sqrt{2}-\dfrac{20}{9}\right).20\approx-4763,88\left(J\right)\)
29 tháng 3 2022
1/2p = 30s
Công gây ra là
\(A=P.h=10m.h=10.50.4=2000\left(J\right)\)
Công suất sinh ra là
\(P=\dfrac{A}{t}=\dfrac{2000}{30}=66,6W\)
Công do lực ma sát sinh ra là
\(A'=F_{ms}.l=30.10=300\left(J\right)\)
Hiệu suất là
\(H=\dfrac{A}{A''}.100\%=\dfrac{2000}{2000+300}.100\%\approx87\%\)
N
19 tháng 4 2022
Công của người đó:
\(A=Fs=300\cdot4=1200\left(J\right)\)
Công suất của người đó:
\(P=\dfrac{A}{t}=\dfrac{1200}{40}=30\)(W)
19 tháng 4 2022
Dùng một ròng rọc động cho ta lợi hai lần về lực và thiệt hai lần về đường đi.
\(\Rightarrow\left\{{}\begin{matrix}F=\dfrac{1}{2}P=\dfrac{1}{2}\cdot300=150N\\s=\dfrac{1}{2}h=\dfrac{1}{2}\cdot4=2m\end{matrix}\right.\)
Công người đó nâng vật lên cao:
\(A=F\cdot s=150\cdot2=300J\)
Công suất thực hiện:
\(P=\dfrac{A}{t}=\dfrac{300}{40}=7,5W\)
VT
12 tháng 3 2018
Đáp án D
- Trọng lượng thùng hàng là:
50.10 = 500 (N)
- Áp dụng công thức:
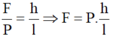
- Lực cần thiết để kéo thùng hàng là:
25 tháng 4 2023
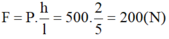
Tóm tắt
\(m=2500kg\)
\(\Rightarrow P=10.m=10.2500=25000N\)
\(h=12m\)
\(t=2p=120s\)
_____________________
a) \(A=?J\)
\(P\left(hoa\right)=?W\)
b) Giải thích?
Giải
a) Công của cần cẩu là:
\(A=P.h=25000.12=300000J\)
Công suất của cần cẩu là:
\(P\left(hoa\right)=\dfrac{A}{t}=\dfrac{300000}{120}=2500W\)
b) Con số 2500W cho ta biết trong 1 giây, cần cẩu thực hiện được công là 2500J
5 tháng 5 2021
1.Công thực hiện được A=P.h=10.m.h=650.10.20=130000 J
=> Công suất của ng công nhân là : P=A/t=130000/120=1083.33 W
2.Công thực hiện được A=F.s=70.800=56000 J
Công suất của người đó là : \(P=\dfrac{A}{t}=\dfrac{F.s}{\dfrac{s}{v}}=F.v=\)70.3,5=245 W
Công của ngừoi đó là
\(A=P.h=10m.h=80.10.5=4000\left(J\right)\)
Công suất là
\(P=\dfrac{A}{t}=\dfrac{4000}{15}=266,7W\)
Công của người đó là:
\(A=P.h=10m.h=10.89.5=4450\left(J\right)\)
Công suất người đó là:
\(P=\dfrac{A}{t}=\dfrac{4450}{15}=\dfrac{890}{3}\left(W\right)\)